시계열 : 농산물 가격 예측 프로젝트 4 (ARIMA 모델을 활용한 시계열 예측 기초와 적용)

qordnswnd123 2025. 1. 30. 22:24

1. 데이터 로드

import pandas as pd
import numpy as np
from IPython.core.display import display, HTML

train_org = pd.read_csv('train.csv')
test_org = pd.read_csv('test.csv')

train_prep = pd.read_csv('train_prep.csv')
test_prep = pd.read_csv('test_prep.csv')

display("train 데이터 원본")
display(train_org.head(5))

print("\n")
display("전처리된 train 데이터")

display(train_prep.head(5))

2. 누락된 날짜 존재 유무와 모든 품목의 가격, 거래량이 0인 행 확인하기

1) 누락된 날짜 비교

train_org['date'] = pd.to_datetime(train_org['date'])
train_prep['date'] = pd.to_datetime(train_prep['date'])

all_dates_org = pd.date_range(start=train_org['date'].min(), end=train_org['date'].max(), freq='D')
missing_dates_org = all_dates_org.difference(train_org['date'])
print(f"train.csv의 누락된 날짜 : {missing_dates_org}")

all_dates_prep = pd.date_range(start=train_prep['date'].min(), end=train_prep['date'].max(), freq='D')
missing_dates_prep = all_dates_prep.difference(train_prep['date'])
print(f"train_prep.csv의 누락된 날짜 : {missing_dates_prep}")

train.csv의 누락된 날짜 : DatetimeIndex(['2021-08-29', '2021-09-05', '2021-09-21', '2021-09-26'], dtype='datetime64[ns]', freq=None)
train_prep.csv의 누락된 날짜 : DatetimeIndex([], dtype='datetime64[ns]', freq='D')

2) 모든 품목의 가격, 거래량이 0인 행 확인하기

features_org = train_org.columns[1:]
all_zero_values_org = train_org[train_org[features_org].apply(lambda row: all(row == 0), axis=1)]
display(f"원본 데이터 : {len(all_zero_values_org)}")

features_prep = train_prep.columns[1:]
all_zero_values_prep = train_prep[train_prep[features_prep].apply(lambda row: all(row == 0), axis=1)]
display(f"전처리 데이터 : {len(all_zero_values_prep)}")

3. 전체 train 데이터에서 실제 학습 기간 및 품목 설정하기

start_date_train = '2021-01'

# 학습 데이터에서 분석기간을 선택하여 추출합니다
train_selected = train_prep[train_prep['date'] >= start_date_train].copy().reset_index(drop=True)

# '배추', '무', '깻잎', '시금치', '토마토', '청상추', 캠벨얼리', '샤인마스캇
item_selected = '배추'

display(f"start date : {train_selected['date'].min().date()}  end date : {train_selected['date'].max().date()}")

'start date : 2021-01-01  end date : 2021-09-27'

4. 특정 품목 차분값에 대한 ACF, PACF그래프 분석 및 신뢰 구간내 LAG값 얻기

※ ACF (AutoCorrelation Function, 자기상관 함수)

ACF는 시계열 데이터에서 하나의 시점의 값이 이전의 여러 시점의 값과 어떤 상관 관계를 가지는지를 측정합니다. 이를 통해 데이터가 얼마나 ‘자기 상관성’을 가지고 있는지 알 수 있습니다. 예를 들어, 주식 가격이 오늘 상승했다면 내일도 상승할 가능성이 있는지, 아니면 전혀 상관이 없는지 등을 알 수 있습니다.

※ PACF (Partial AutoCorrelation Function, 부분 자기상관 함수)

PACF는 시점 t와 t-n사이의 상관 관계를, t-1, t-2...(t-n-1)과의 상관 관계를 배제하고 측정합니다. 즉, 중간에 있는 다른 시점의 영향을 제거한 상태에서 두 시점의 상관 관계를 측정합니다.

예를 들어, 주식 가격이 오늘 상승했을 때 5일 후에도 상승하는 경향이 있는지를 알고 싶다면, 1일, 2일, 3일, 4일 후의 영향을 배제한 상태에서 오늘과 5일 후의 상관 관계를 측정할 수 있습니다.

1) 특정 품목 1차 차분값에 대한 ACF, PACF그래프 분석

train_selected의 'date'컬럼을 제외한 데이터에 대하여 차분을 수행합니다.
자기 상관함수를 그립니다.
부분 자기상관 함수를 그립니다

import matplotlib.pyplot as plt
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf

n_diff = 1
features = train_selected.columns[1:]
train_selected_diff = train_selected[features].diff(n_diff).dropna()

fig, ax = plt.subplots(1,2 ,figsize = (12, 4))

# ACF (AutoCorrelation Function) 그래프 그리기
plot_acf(train_selected_diff[f'{item_selected}_가격'], lags=50, title=f'ACF ({item_selected}_가격)', ax=ax[0])

# PACF (Partial AutoCorrelation Function) 그래프 그리기
plot_pacf(train_selected_diff[f'{item_selected}_가격'], lags=50, title=f'PACF ({item_selected}_가격)', ax=ax[1])

plt.tight_layout()

※ 결과 해석

차분 이후 ACF와 PACF 그래프에서 특성 lag값 이후에 신뢰구간 영역으로 급격히 상관관계가 줄어든것을 관찰할 수 있고 이는 정상성을 가지는 데이터가 가지는 특성으로 볼수 있으면 ARIMA와 같은 통계기반의 시계열 모델을 적용하기에 적절합니다.

2) 신뢰구간내 acf, pacf값 이용하여 ARIMA 모델의 p(AR 모델), q(MA 모델) 파라미터 선택 가이드

※ MA(q) 모델의 q 값 선정

ACF 그래프에서 값이 '급격히' 0으로 떨어지는 시차(lag)를 찾습니다. 예를 들어, ACF 그래프에서 2시차까지는 상당한 상관성이 있고, 3시차부터는 거의 0에 가깝게 된다면, q=2로 설정할 수 있습니다.

※ AR(p) 모델의 p 값 선정

PACF 그래프를 확인합니다. PACF 그래프에서 값이 '급격히' 0으로 떨어지는 시차(lag)를 찾습니다. 예를 들어, PACF 그래프에서 1시차까지는 상당한 상관성이 있고, 2시차부터는 거의 0에 가까워진다면, p=1로 설정할 수 있습니다.

이러한 방식으로 ACF와 PACF 그래프를 활용해 ARIMA 모델의 p와 q 값을 초기 추정할 수 있습니다. 이는 가이드라인에 불과하며, 실제 데이터에 대해 여러 파라미터를 시도해보고 최적의 값을 찾는 과정이 필요합니다.

from statsmodels.tsa.stattools import acf, pacf

acf_values = acf(train_selected_diff[f'{item_selected}_가격'], nlags=50)
pacf_values = pacf(train_selected_diff[f'{item_selected}_가격'], nlags=50)

# 신뢰 구간 계산 (95% 신뢰 구간)
confidence_interval = 1.96 / np.sqrt(len(train_selected_diff))

q_param = []
for lag, value in enumerate(acf_values):
    if np.abs(value) > confidence_interval:
        q_param.append(lag)

p_param = []
for lag, value in enumerate(pacf_values):
    if np.abs(value) > confidence_interval:
        p_param.append(lag)


display(f"Q parameters of MA model is {q_param},  P of AR model is {p_param}")

'Q parameters of MA model is [0, 1, 7, 14, 25, 29],  P of AR model is [0, 1, 6, 25, 29, 31, 44]'

※ 결과 해석

품목 가격 데이터는 1차 차분을 통해 정상성이 확보되었습니다. 이를 바탕으로 ACF(AutoCorrelation Function)와 PACF(Partial AutoCorrelation Function) 분석을 수행하였습니다.

[배추의 경우]

MA 모델의 q 파라미터는 ACF 분석에서 자기상관이 0에 근접하게 되는 첫 번째 래그값 (1) 혹은 두 번째 래그값 (7)을 선택하는 것을 생각해볼 수 있습니다.

비슷하게, AR 모델의 p 파라미터 역시 PACF 분석을 통해 자기상관이 0에 근접하는 첫 번째 래그값 (3) 혹은 두 번째 래그값 (6)을 선택하는 것을 생각해볼 수 있습니다. 이렇게 정해진 p와 q 파라미터는 ARIMA 모델의 초기 설정 값으로 사용될 예정입니다.

5. 1,2,4주 후 가격 예측을 위한 학습 데이터 생성

from datetime import timedelta
# 'true_1week', 'true_2week', 'true_4week' 컬럼을 생성하기 위한 함수
def generate_target_columns(df, date_col, item , week):

    item_price_name = f'{item}_가격'
    target_price_name = f'true_{week}week'
    target_date_name = f'date_{week}week'

    for i, row in df.iterrows():

        target_date = row[date_col] + pd.DateOffset(weeks=week)
        target_value = df.loc[df[date_col] == target_date, item_price_name]

        if not target_value.empty:
            df.at[i, target_date_name] = target_date.date()
            df.at[i, target_price_name] = target_value.values[0]

        else:
            df.at[i, target_date_name] = np.nan
            df.at[i,target_price_name] = np.nan


    df = df.dropna().reset_index(drop=True)

    return df

# 1,2,4주 후를 예측하는 모델에 필요한 학습, 검증을 위한 데이터를 각각 생성합니다.
train_1week = train_selected[['date',f'{item_selected}_가격' ]].copy()
train_2week = train_selected[['date',f'{item_selected}_가격' ]].copy()
train_4week = train_selected[['date',f'{item_selected}_가격' ]].copy()


#1,2,4주 후를 예측하는 모델에 필요한 학습, 검증을 위한 데이터에 정답지 컬럼을 생성합니다.
train_1week = generate_target_columns(train_1week, 'date', item_selected, 1)
train_2week = generate_target_columns(train_2week, 'date', item_selected, 2)
train_4week = generate_target_columns(train_4week, 'date', item_selected, 4)

# 어떤 컬럼이 생성 되었는지 각각 확인
display(train_1week.columns)
display(train_2week.columns)
display(train_4week.columns)

# 생성된 컬럼 확인
display(train_1week.head(10))

6. ARIMA 모델 학습 및 성능 요약을 통한 예측 성능 분석

1) ACF, PACF 그래프 해석 기반 ARIMA 모델 파라미터 (p, d, q) 초기 설정

Arima 모델에 학습 시키는 데이터의 'date'을 index로 설정합니다.
ARIMA 모델을 생성합니다. 이때 ARIMA 모델의 (p,d,q)파라미터는 위에서 분석한 결과를 기반으로 적절하게 선택합니다.
ARIMA 모델의 summary() 함수를 이용하여 모델 적합 결과를 출력합니다.

from statsmodels.tsa.arima.model import ARIMA
# 경고 메시지를 숨기기 위해 코드 블록 추가
import warnings
warnings.filterwarnings('ignore')

start_date_valid = '2021-05-01'

_train_item = train_1week[train_1week['date'] < start_date_valid].reset_index(drop=True)
_valid_item = train_1week[train_1week['date'] >= start_date_valid].reset_index(drop=True)

train_item_arima = _train_item.copy()
train_item_arima.set_index('date', inplace=True)  # 'date' 컬럼을 인덱스로 설정

model_arima = ARIMA(train_item_arima[f"{item_selected}_가격"], order=(7, 1, 6))  # AR(7), I(1), MA(6) 모델 설정

fit_result = model_arima.fit()  # 모델 학습
display(fit_result.summary())  # 모델 결과 출력

※ 주요 summary() 결과에 대한 의미

AIC (Akaike Information Criterion):

AIC는 모델의 복잡성과 적합도를 동시에 고려하는 지표입니다.
AIC 값이 낮을수록 모델이 데이터에 잘 적합되었다고 볼 수 있습니다.

BIC (Bayesian Information Criterion):

BIC 역시 AIC와 유사하게 모델의 복잡성과 적합도를 고려하지만, 샘플 크기에 더 엄격한 패널티를 부과합니다.
BIC 값도 낮을수록 좋습니다.

ar.L1, ma.L1

ar.L1값은 ARIMA 모델 중 AR(AutoRegressive) 부분의 1번째 래그(lag)에 대한 계수입니다.
AR 모델은 이전 n개의 시점의 데이터가 현재 시점의 데이터에 얼마나 영향을 미치는지를 설명합니다.
여기서 ar.L1은 한 시점 전의 데이터가 현재 시점의 데이터에 미치는 영향을 나타냅니다.
ma.L1값은 MA(Moving Average) 부분의 1번째 래그(lag)에 대한 계수입니다.
MA 모델은 이전 n개의 시점의 오차(잔차)가 현재 시점의 데이터에 얼마나 영향을 미치는지를 설명합니다.

P>|z|

이는 각 계수의 유의성을 검정하는 p-value입니다.
반적으로 0.05 이하일 때 해당 계수는 통계적으로 유의미하다고 판단할 수 있습니다.
ar.L1, ma.L1 모두 0에 가까운 값이라면 유의미하다고 볼 수 있습니다.

Ljung-Box (Q):

잔차의 자기상관을 검정하는 지표입니다.
Prob(Q) 값이 높을수록 모델의 잔차가 자기상관을 가지지 않는다고 판단합니다.
Prob(Q) > 0.05라면 잔차가 무작위적이라고 볼 수 있습니다.
잔차에 자기상관이 없다면 이는 모델이 데이터의 패턴을 잘 반영하고 있다는 의미입니다.
잔차에 자기상관이 있다면 이는 모델이 데이터의 패턴을 완전히 반영하지 못했다는 의미로 해석할 수 있습니다.

파라미터를 변화 시켜가며 AIC값을 관할합니다. AIC 값이 낮을수록 모델이 데이터에 잘 적합되었다고 볼 수 있습니다.

2) ARIMA 모델 최적 파라미터 (P,D,Q) 찾기

주어진 범위 내에서 가능한 모든 (p,d,q) 조합에 대해 ARIMA 모델을 적합시켜 가장 낮은 AIC 값을 가진 모델을 찾습니다

적합된 모델의 AIC 값을 출력합니다
모델의 AIC 값을 리스트에 추가합니다
계산된 AIC 값들 중 최소값을 가지는 파라미터를 찾습니다

import itertools
import warnings
warnings.filterwarnings('ignore')

# p, d, q 범위 설정
p = range(0, 7)
d = range(1, 2)
q = range(0, 3)

# 가능한 모든 p, d, q 조합 생성
pdq = list(itertools.product(p, d, q))

# AIC 값을 저장할 리스트 초기화
aic = []

train_item_arima = _train_item.copy()
train_item_arima.set_index('date', inplace = True)


# 각 조합에 대해 ARIMA 모델 적합 및 AIC 계산
for i in pdq:
    try:
        # 모델 생성 및 적합
        model = ARIMA(train_item_arima[f"{item_selected}_가격"], order=i)  # 빈도를 'B' (영업일)로 설정
        model_fit = model.fit()

        # AIC 값 출력 및 저장
        print(f'ARIMA : {i} >> AIC : {round(model_fit.aic, 2)}')
        aic.append(round(model_fit.aic, 2))
    except:
        continue

optimal_pdq_info = [ (pdq[i], j) for i, j in enumerate(aic) if j == min(aic)]
optimal_pdq = optimal_pdq_info[0][0]
display(f"optimal pdq parameter : {optimal_pdq_info}")

ARIMA : (0, 1, 0) >> AIC : 1396.25
ARIMA : (0, 1, 1) >> AIC : 1397.45
ARIMA : (0, 1, 2) >> AIC : 1378.85
ARIMA : (1, 1, 0) >> AIC : 1397.98
ARIMA : (1, 1, 1) >> AIC : 1383.4
ARIMA : (1, 1, 2) >> AIC : 1378.5
ARIMA : (2, 1, 0) >> AIC : 1387.26
ARIMA : (2, 1, 1) >> AIC : 1378.86
ARIMA : (2, 1, 2) >> AIC : 1380.14
ARIMA : (3, 1, 0) >> AIC : 1388.66
ARIMA : (3, 1, 1) >> AIC : 1380.42
ARIMA : (3, 1, 2) >> AIC : 1382.1
ARIMA : (4, 1, 0) >> AIC : 1389.76
ARIMA : (4, 1, 1) >> AIC : 1379.7
ARIMA : (4, 1, 2) >> AIC : 1383.49
ARIMA : (5, 1, 0) >> AIC : 1360.47
ARIMA : (5, 1, 1) >> AIC : 1361.47
ARIMA : (5, 1, 2) >> AIC : 1356.71
ARIMA : (6, 1, 0) >> AIC : 1360.49
ARIMA : (6, 1, 1) >> AIC : 1359.88
ARIMA : (6, 1, 2) >> AIC : 1355.34

'optimal pdq parameter : [((6, 1, 2), 1355.34)]'

7. ARIMA 모델을 이용한 1,2,4주 후 가격 예측

warnings.filterwarnings('ignore')

feature = f"{item_selected}_가격"

_train_data_1week = train_1week[ train_1week['date'] < start_date_valid].reset_index(drop=True)
_valid_data_1week  = train_1week[ train_1week['date'] >= start_date_valid].reset_index(drop=True)

_train_data_2week = train_2week[ train_2week['date'] < start_date_valid].reset_index(drop=True)
_valid_data_2week  = train_2week[ train_2week['date'] >= start_date_valid].reset_index(drop=True)

_train_data_4week = train_4week[ train_4week['date'] < start_date_valid].reset_index(drop=True)
_valid_data_4week  = train_4week[ train_4week['date'] >= start_date_valid].reset_index(drop=True)

model_1week = ARIMA(_train_data_1week[feature], order=optimal_pdq)
fit_1week = model_1week.fit()
y_pred_1week = fit_1week.forecast(steps=7)

model_2week = ARIMA(_train_data_2week[feature], order=optimal_pdq)
fit_2week = model_2week.fit()
y_pred_2week = fit_2week.forecast(steps=14)

model_4week = ARIMA(_train_data_4week[feature], order=optimal_pdq)
fit_4week = model_4week.fit()
y_pred_4week = fit_4week.forecast(steps=28)

display(f"1주(7일)간 예측 가격 : {y_pred_1week.values}")
display(f"2주(14일간 예측 가격 : {y_pred_2week.values}")
display(f"4주(28일)간 예측 가격 : {y_pred_4week.values}")

'1주(7일)간 예측 가격 : [831.92892376 820.2783824  734.84512827 760.31882731 772.0605311\n 693.70876406 697.00452349]'

'2주(14일간 예측 가격 : [831.92892376 820.2783824  734.84512827 760.31882731 772.0605311\n 693.70876406 697.00452349 796.07079657 786.65465761 726.23752052\n 759.64721645 780.0758945  715.70238638 714.05137229]'

'4주(28일)간 예측 가격 : [831.92892376 820.2783824  734.84512827 760.31882731 772.0605311\n 693.70876406 697.00452349 796.07079657 786.65465761 726.23752052\n 759.64721645 780.0758945  715.70238638 714.05137229 782.10887954\n 770.2041156  725.01946286 757.89666203 777.91839673 727.75924837\n 724.90658915 774.57790503 762.10662686 727.35243997 756.11918613\n 773.41699245 734.43089373 732.11657068]'

8. 검증 기간 첫째날을 포함한 ARIMA 모델로 1주, 2주, 4주 후 가격 예측하기

검증 데이터셋(_valid_data_1week)에서 첫 번째 날짜의 데이터를 _valid_day1에 저장하고, 학습 데이터셋 _train_item에 _valid_day1을 추가(concat)하여 새로운 학습 데이터셋 _train_valid_day1을 생성합니다.

이 코드의 주된 의도는 실시간으로 업데이트되는 최신 데이터를 활용하여 ARIMA 모델을 훈련시키고 예측하는 것입니다. 이러한 방식의 가장 큰 장점은 모델이 최신 시장 상황이나 다른 동적 요소를 빠르게 반영할 수 있다는 것입니다. 즉, 과거의 학습된 패턴보다 새로운 패턴을 더 빠르게 적용할 수 있다는 장점이지만 이러한 방법에는 몇 가지 주의할 점이 있습니다.

첫째, 매일 모델을 업데이트하려면 상당한 계산 리소스가 필요할 수 있으며 실행 시간이나 비용 측면에서 부담이 될 수 있습니다.

둘째, 너무 자주 모델을 업데이트하면 특히, 데이터 노이즈까지 학습할 위험이 있어 과적합이 발생할 수 있습니다.

마지막으로, 데이터를 지속적으로 업데이트하고 관리해야 하므로 데이터 관리가 복잡해질 수 있습니다.

warnings.filterwarnings('ignore')

# 검증기간 첫째날 데이터 합치기
_valid_day1 = _valid_data_1week.iloc[[0]]

_train_update_1week = pd.concat([ _train_data_1week, _valid_day1 ] )
_train_update_2week = pd.concat([ _train_data_2week, _valid_day1 ] )
_train_update_4week = pd.concat([ _train_data_4week, _valid_day1 ] )

feature = f"{item_selected}_가격"

model_1week = ARIMA(_train_update_1week[feature], order=optimal_pdq)
fit_1week = model_1week.fit()
y_pred_1week = fit_1week.forecast(steps=7)

model_2week = ARIMA(_train_update_2week[feature], order=optimal_pdq)
fit_2week = model_2week.fit()
y_pred_2week = fit_2week.forecast(steps=14)

model_4week = ARIMA(_train_update_4week[feature], order=optimal_pdq)
fit_4week = model_4week.fit()
y_pred_4week = fit_4week.forecast(steps=28)

display(f"1주(7일)간 예측 가격 : {y_pred_1week.values}")
display(f"2주(14일간 예측 가격 : {y_pred_2week.values}")
display(f"4주(28일)간 예측 가격 : {y_pred_4week.values}")

'1주(7일)간 예측 가격 : [659.36150871 614.83096521 670.01720387 696.33824653 663.53328847\n 645.59474644 663.09778994]'

'2주(14일간 예측 가격 : [659.36150871 614.83096521 670.01720387 696.33824653 663.53328847\n 645.59474644 663.09778994 658.04095812 636.31584796 659.47005062\n 680.56195121 658.42228919 647.7976406  666.28077382]'

'4주(28일)간 예측 가격 : [659.36150871 614.83096521 670.01720387 696.33824653 663.53328847\n 645.59474644 663.09778994 658.04095812 636.31584796 659.47005062\n 680.56195121 658.42228919 647.7976406  666.28077382 661.87025994\n 643.96164259 657.7356565  672.6291373  656.81871309 650.05535495\n 665.4361915  662.72630482 648.47309811 657.49008772 668.30016048\n 656.68939544 651.89930511 663.9853606 ]'

9. 평가 산식 NMAE (Normalized Mean Absolute Error)

※ NMAE

MAE (Mean Absolute Error)는 예측값과 실제값의 절대적인 차이를 평균으로 나타내는 매우 직관적인 측정 방법입니다. 그러나 MAE는 단위나 스케일에 따라 해석이 달라질 수 있습니다. 예를 들어, 가격 예측의 경우 MAE 값이 10일 때, 이 값이 상품의 가격이 일반적으로 수천 단위라면 문제가 없을 수 있지만, 가격이 10~20 단위라면 큰 문제가 될 수 있습니다.

이와 같은 문제를 해결하기 위해 NMAE (Normalized Mean Absolute Error)가 사용될 수 있습니다. NMAE는 각 개별 오차를 해당 실제 값으로 나눠 정규화합니다. 이렇게 하면 오차가 실제 값에 대해 얼마나 비율을 차지하는지를 측정할 수 있어, 스케일이나 단위에 덜 민감하게 됩니다. 그 결과, 다양한 스케일이나 단위를 가진 여러 변수를 비교 분석하기 쉬워집니다.

NMAE는 특히 다음과 같은 경우에 유용합니다.

다양한 스케일의 변수 비교: 여러 변수가 서로 다른 스케일이나 단위를 가지고 있을 때 NMAE를 사용하면, 하나의 일관된 기준으로 성능을 비교할 수 있습니다.
비율로의 해석: NMAE 값은 비율 해석이 쉽고, 오차가 전체 값에 차지하는 비중을 쉽게 이해할 수 있습니다.
0 근접성: NMAE가 0에 가까울수록 모델의 성능이 좋다고 판별할 수 있어, 직관적인 해석이 가능합니다.

그렇지만 NMAE에도 단점이 있는데, 특히 실제 값이 0에 가까운 경우에는 오차가 비정상적으로 커질 가능성이 있습니다. 이를 방지하기 위해 실제 값이 0인 경우는 계산에서 제외하는 등의 전처리가 필요할 수 있습니다.

# NMAE (Normalized Mean Absolute Error)를 계산하는 함수 정의
def nmae(true_values, pred_values):

    # NMAE (Normalized Mean Absolute Error) 계산
    # NMAE = (1/n) * Σ(|true_value - pred_value| / true_value)

    mask = true_values != 0

    filtered_true_values = true_values[mask]
    filtered_pred_values = pred_values[mask]

    return np.sum(np.abs(filtered_true_values - filtered_pred_values) / filtered_true_values) / len(filtered_true_values)

# 예제: 실제 가격과 예측 가격 데이터
true_values = np.array([100, 200, 300, 400, 0])  # 실제 가격
pred_values = np.array([110, 190, 320, 390, 0])  # 예측 가격

# NMAE 계산
nmae_result = nmae(true_values, pred_values)
nmae_result

0.06041666666666667

10. 매일 업데이트된 데이터로 1, 2, 4주 후 가격 예측하는 ARIMA 모델에 대한 성능 검증 함수 구현

매일 업데이트되는 최신 데이터를 활용하여 1주, 2주, 4주 후의 가격을 예측하는 ARIMA 모델의 성능을 검증하는 함수를 구현하고, 실제 검증 과정을 수행해 보겠습니다.
함수는 매일 수집되는 최신 데이터를 통합하여 학습 데이터를 업데이트하고, 이를 바탕으로 지정한 검증일로부터의 예측 성능을 NMAE(Normalized Mean Absolute Error) 지표로 평가합니다.

from statsmodels.tsa.arima.model import ARIMA
from tqdm import tqdm

warnings.filterwarnings('ignore')

def evaluate_arima_model(item_name, df, start_date, n_week, pdq , nmae_function):

    true_week_lst,pred_week_lst,date_week_lst = [],[],[]

    feature = f"{item_name}_가격"
    target_price_col = f'true_{n_week}week'

    # 학습 및 검증 데이터 분리
    _train_data = df[df['date'] < start_date].reset_index(drop=True)
    _valid_data = df[df['date'] >= start_date].dropna().reset_index(drop=True)

    valid_day_lst = _valid_data['date'].to_list()

    for date in tqdm(valid_day_lst):

        valid_updated = _valid_data[_valid_data['date'] <= date]
        train_updated = pd.concat([ _train_data, valid_updated ] )
        train_updated.set_index('date', inplace = True)

        # 매일 train 데이터 업데이트하고, 1주후 가격 예측하기
        model_week = ARIMA(train_updated[feature], order=optimal_pdq)
        fit_week = model_week.fit()
        forecast_week = fit_week.forecast(steps=7*n_week)

        true_week_lst.append(df.loc[df['date'] == date, target_price_col].values[0])
        pred_week_lst.append(forecast_week.iloc[-1])

    score_week = nmae_function( np.array(true_week_lst) , np.array(pred_week_lst))

    return score_week, pred_week_lst

start_valid_date = '2021-05-01'

score_1week, pred_1week = evaluate_arima_model(item_selected, train_1week, start_valid_date, 1, optimal_pdq, nmae)
score_2week, pred_2week = evaluate_arima_model(item_selected, train_2week, start_valid_date, 2, optimal_pdq, nmae)
score_4week, pred_4week = evaluate_arima_model(item_selected, train_4week, start_valid_date, 4, optimal_pdq, nmae)

score_mean = (score_1week + score_2week + score_4week) / 3

display(f'mean nmae score : {score_mean} ({score_1week},{score_2week},{score_4week})')

100%|██████████| 143/143 [00:33<00:00,  4.24it/s]
100%|██████████| 136/136 [00:30<00:00,  4.44it/s]
100%|██████████| 122/122 [00:27<00:00,  4.47it/s]

'mean nmae score : 0.21128415209206683 (0.1773355974288565,0.21465636336847313,0.2418604954788709)'

11. ARIMA 모델을 활용한 가격 예측 그래프 시각화

1) ARIMA 모델의 1주후 가격 예측 시각화

import matplotlib.pyplot as plt

predicted_1week_df = pd.DataFrame({'date_1week': list(_valid_data_1week['date_1week']), 'pred_1week': pred_1week}).dropna()

start_day_valid = _valid_data_1week['date'].min()

# 그래프 그리기
plt.figure(figsize=(12, 4))
plt.plot(train_selected['date'], train_selected[f'{item_selected}_가격'], label='Real', color='blue')
plt.plot(predicted_1week_df['date_1week'], predicted_1week_df['pred_1week'], label='Predicted 1week', color='orange',linestyle='--')

plt.axvline(x=(start_day_valid), color='r', linestyle='--', label='Start of Validation')

plt.title('실가격 vs 예측가격')

plt.tight_layout()
plt.show()

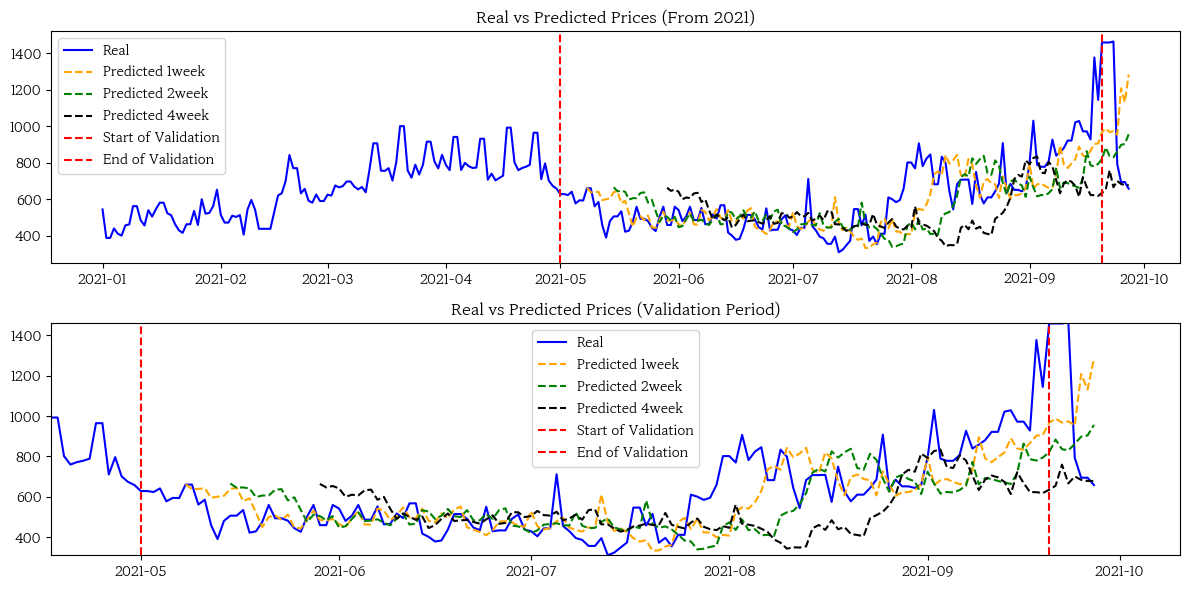
2) ARIMA 모델을 이용한 예측 거동 시각화 함수 생성과 실제 가격과의 비교

이 코드는 ARIMA 모델의 예측 거동을 시각화하는 함수를 생성하고, 이 함수를 통해 실제 가격과 1주, 2주, 4주 후의 예측 가격을 비교하는 그래프를 그립니다. 이렇게 함으로써 모델의 성능을 시각적으로 쉽게 이해하고 평가할 수 있습니다.

import matplotlib.pyplot as plt
import pandas as pd


def plot_predict_behavior(df_all, df_valid_week1, df_valid_week2, df_valid_week4, pred_1week, pred_2week, pred_4week, item_selected):

    predicted_1week_df = pd.DataFrame({'date_1week': list(df_valid_week1['date_1week']), 'pred_1week': pred_1week}).dropna()
    predicted_2week_df = pd.DataFrame({'date_2week': list(df_valid_week2['date_2week']), 'pred_2week': pred_2week}).dropna()
    predicted_4week_df = pd.DataFrame({'date_4week': list(df_valid_week4['date_4week']), 'pred_4week': pred_4week}).dropna()

    start_date_valid = df_valid_week1['date'].min()
    end_date_valid = df_valid_week1['date'].max()

    plt.figure(figsize=(12, 6))

    # 전체 기간 그래프
    plt.subplot(2, 1, 1)
    plt.plot(df_all['date'], df_all[f'{item_selected}_가격'], label='Real', color='blue')
    plt.plot(predicted_1week_df['date_1week'], predicted_1week_df['pred_1week'], label='Predicted 1week', color='orange', linestyle='--')
    plt.plot(predicted_2week_df['date_2week'], predicted_2week_df['pred_2week'], label='Predicted 2week', color='green', linestyle='--')
    plt.plot(predicted_4week_df['date_4week'], predicted_4week_df['pred_4week'], label='Predicted 4week', color='black', linestyle='--')
    plt.axvline(x=start_date_valid, color='r', linestyle='--', label='Start of Validation')
    plt.axvline(x=end_date_valid, color='r', linestyle='--', label='End of Validation')
    plt.title('Real vs Predicted Prices (From 2021)')
    plt.legend()

    y_min_zoomed_graph = min(df_valid_week1[f'{item_selected}_가격'].min(),
                             predicted_1week_df['pred_1week'].min(),
                             predicted_2week_df['pred_2week'].min(),
                             predicted_4week_df['pred_4week'].min())

    y_max_zoomed_graph = max(df_valid_week1[f'{item_selected}_가격'].max(),
                             predicted_1week_df['pred_1week'].max(),
                             predicted_2week_df['pred_2week'].max(),
                             predicted_4week_df['pred_4week'].max())

    # 검증 기간 확대 그래프
    plt.subplot(2, 1, 2)
    plt.plot(df_all['date'], df_all[f'{item_selected}_가격'], label='Real', color='blue')
    plt.plot(predicted_1week_df['date_1week'], predicted_1week_df['pred_1week'], label='Predicted 1week', color='orange', linestyle='--')
    plt.plot(predicted_2week_df['date_2week'], predicted_2week_df['pred_2week'], label='Predicted 2week', color='green', linestyle='--')
    plt.plot(predicted_4week_df['date_4week'], predicted_4week_df['pred_4week'], label='Predicted 4week', color='black', linestyle='--')
    plt.axvline(x=start_date_valid, color='r', linestyle='--', label='Start of Validation')
    plt.axvline(x=end_date_valid, color='r', linestyle='--', label='End of Validation')
    plt.xlim(left=start_date_valid - pd.DateOffset(days=14))
    plt.ylim(top=y_max_zoomed_graph, bottom=y_min_zoomed_graph)
    plt.title('Real vs Predicted Prices (Validation Period)')
    plt.legend()

    plt.tight_layout()
    plt.show()

plot_predict_behavior(train_selected, _valid_data_1week, _valid_data_2week, _valid_data_4week, pred_1week, pred_2week, pred_4week, item_selected