인구 소득 예측 프로젝트 3 : 이상치 처리

qordnswnd123 2024. 12. 31. 19:56

1. Interquartile Range(IQR) 방법을 사용한 'capital.gain' 및 'capital.loss' 피처의 이상치 검출과 시각화

def out_iqr(df, column):
    # 퀀타일 함수와 IQR 계산을 적용합니다.
    q25, q75 = np.quantile(df[column], 0.25), np.quantile(df[column], 0.75)
    iqr = q75 - q25
    lower, upper = q25 - (iqr * 1.5), q75 + (iqr * 1.5)

    # 이상치 개수 계산
    df1 = df[df[column] > upper]
    df2 = df[df[column] < lower]
    total_outliers = df1.shape[0] + df2.shape[0]

    # 결과 반환
    return iqr, lower, upper, total_outliers

# 이상치 확인 및 시각화
fig, axes = plt.subplots(1, 2, figsize=(10, 3))

iqr_cg, lower_cg, upper_cg, total_outliers_cg = out_iqr(train, 'capital.gain')
sns.distplot(train['capital.gain'], kde=False, ax=axes[0])

iqr_cl, lower_cl, upper_cl, total_outliers_cl = out_iqr(train, 'capital.loss')
sns.distplot(train['capital.loss'], kde=False, ax=axes[1])

plt.show()

# 결과 출력
print('capital.gain의 IQR 값은', iqr_cg)
print('capital.gain의 하한값은', lower_cg)
print('capital.gain의 상한값은', upper_cg)
print('capital.gain의 이상치 개수는', total_outliers_cg, '개입니다.\n')

print('capital.loss의 IQR 값은', iqr_cl)
print('capital.loss의 하한값은', lower_cl)
print('capital.loss의 상한값은', upper_cl)
print('capital.loss의 이상치 개수는', total_outliers_cl, '개입니다.')

※ 결과 해석

capital.gain에 대한 해석:
이상치를 찾기 위해 사용된 IQR(Interquartile Range)은 0입니다. 이는 25% 분위수(Q1)와 75% 분위수(Q3) 사이에 변동이 없음을 의미합니다. 하한값과 상한값 또한 0입니다.
따라서, 모든 값은 같은 이상치로 간주됩니다. 총 389개의 이상치가 있습니다.
capital.loss에 대한 해석:
capital.gain과 마찬가지로, IQR은 0입니다. 하한값과 상한값 또한 0입니다.
따라서, 모든 값은 같은 이상치로 간주됩니다. 총 167개의 이상치가 있습니다.

IQR 방법을 사용하여 이상치를 식별하는 것은 일반적인 방법 중 하나입니다.

그러나 이 경우에는 대부분의 값이 0 주위에 집중되어 있고, 소수의 값들이 극단적으로 높은 값을 가지기 때문에 이 방법이 효과적이지 않을 수 있습니다.

이러한 경우에는 다음과 같은 방법을 고려할 수 있습니다:

1) Z-Score 방법: 각 데이터 포인트가 평균으로부터 표준 편차 몇 배만큼 떨어져 있는지를 측정합니다.
2) 로그 변환(log transform): 데이터에 로그 변환을 적용하여 값의 범위를 줄일 수 있습니다. 이는 이상치의 영향을 줄이는 데 도움이 될 수 있습니다.
3) 도메인 지식 활용: 해당 분야의 전문가의 도움을 받아 이상치를 식별하거나, 도메인 지식을 활용하여 이상치를 처리할 수 있습니다.

2. 이상치 처리를 위한 데이터 변환 및 왜도(Skewness) 시각화

✔ 로그 변환:
로그 변환은 데이터의 값에 자연 로그(밑이 e인 로그)를 취하는 것으로, 주로 데이터의 분포를 정규 분포에 가깝게 만드는 데 사용됩니다. np.log1p 함수는 각 데이터 포인트에 1을 더한 후 로그를 취하는 함수로, 이렇게 하면 0 또는 음수 값에 대한 문제를 피할 수 있습니다.

로그 변환은 큰 값을 가진 데이터의 영향을 줄이고, 데이터의 스케일을 줄이는 데도 효과적입니다.

✔ Box-Cox 변환:
Box-Cox 변환은 양수 데이터에 대해 정규 분포에 가깝게 만들기 위한 통계적 변환 방법 중 하나입니다.
scipy.stats.boxcox 함수는 Box-Cox 변환을 수행하며, 이 함수는 입력받은 데이터를 수학적으로 변환하여 정규 분포에 가깝게 만듭니다. 변환된 값은 boxcox_data에 저장됩니다.

Box-Cox 변환은 이상치의 영향을 줄이고 데이터의 분포를 정규화하는 데 유용합니다.

✔ 제곱근 변환:
제곱근 변환은 데이터의 값을 해당 값의 제곱근으로 변환하는 방법입니다. 주로 데이터의 분포를 정규화하는 데 사용됩니다.

제곱근 변환은 특히 0 또는 양수 값만 포함된 데이터에 사용하며, 데이터의 분포를 정규화하고 이상치의 영향을 줄이는 데 도움이 됩니다.

from scipy import stats

transformations = ["원본 데이터", "로그 변환", "Box-Cox 변환", "제곱근 변환"]
variables = ["capital.gain", "capital.loss"]
colors = ['b', 'y', 'r', 'g']

fig, axes = plt.subplots(4, 2, figsize=(10,10))

for i, var in enumerate(variables):
    
    # 데이터 변환
    log_data = np.log1p(train[var])
    boxcox_data = pd.Series(stats.boxcox(train[var] + 1)[0]) 
    sqrt_data = np.sqrt(train[var])
    data_list = [train[var], log_data, boxcox_data, sqrt_data]

    # 시각화
    for j, data in enumerate(data_list):
        sns.histplot(data, kde=True, ax=axes[j, i], color=colors[j], bins=30)
        axes[j, i].set_title(f"{variables[i]} - {transformations[j]} (Skewness: {data.skew():.2f})")
        axes[j, i].set_xlabel('')
        axes[j, i].set_ylabel('')

plt.tight_layout()
plt.show()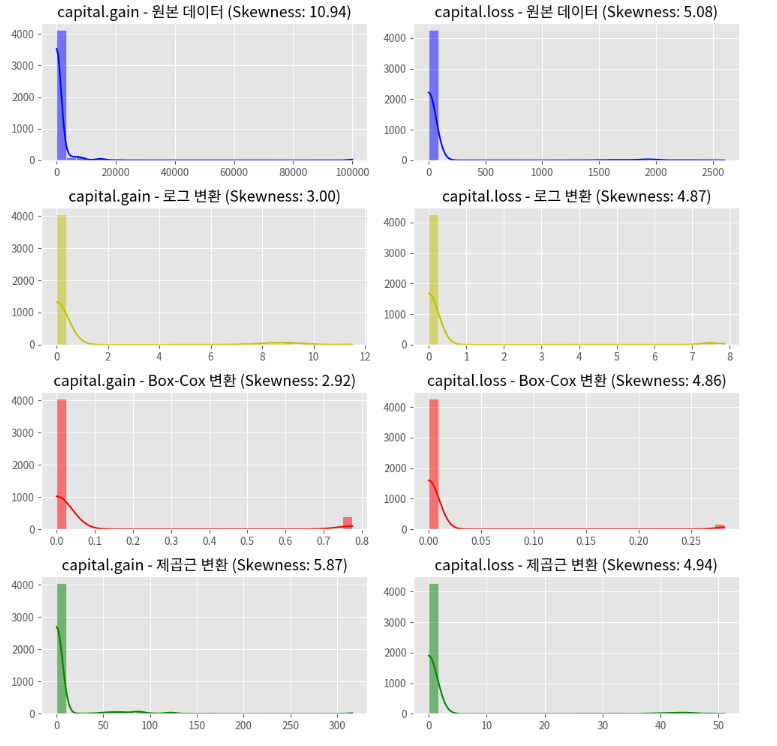

※ 결과 해석

1) capital.gain
원본 데이터: 왜도가 매우 높습니다. 대부분의 값이 0 주변에 집중되어 있으며, 이상치가 존재합니다.
로그 변환: 왜도가 줄어들었으나 여전히 높은 편입니다. 데이터 분포가 약간 개선되었습니다.
Box-Cox 변환: 왜도가 더 줄어들어 데이터 분포가 더 정규화되었습니다.
제곱근 변환: 왜도가 줄어들었으나 Box-Cox 변환만큼은 아닙니다.

2) capital.loss
원본 데이터: 'capital.gain'과 마찬가지로, 왜도가 매우 높으며 대부분의 값이 0 주변에 집중되어 있습니다.
로그 변환: 왜도가 줄어들었으나 여전히 높은 편입니다.
Box-Cox 변환: 왜도가 더 줄어들어 데이터 분포가 더 정규화되었습니다.
제곱근 변환: 왜도가 줄어들었으나 Box-Cox 변환만큼은 아닙니다.

3. Z-Score를 사용한 Capital Gain 및 Loss 이상치 검출과 시각화

※ 이상치 탐지와 Z-점수

Z-점수가 특정 임계값 이상이면 해당 데이터 포인트는 이상치로 간주될 수 있습니다.

통계적으로는 Z-점수가 ±3 정도를 넘어가면 이상치로 취급하는 경우가 많습니다.

이는 정규 분포에서 99.7%의 데이터가 평균에서 ±3 표준편차 범위에 존재하는 경향이 있기 때문입니다.

예를 들어, Z-점수가 3보다 크면 해당 데이터 포인트는 평균에서 3 표준편차 이상 떨어져 있는 것이므로 이상치로 간주될 가능성이 높습니다. 반대로, Z-점수가 -3보다 작으면 마찬가지로 이상치로 간주할 수 있습니다.

✔ 이상치 탐지를 위해 Z-점수를 사용하는 것은 데이터의 분포가 정규 분포에 가까울 때 특히 효과적입니다.

만약 데이터가 정규 분포와 다소 차이가 있다면, 다른 이상치 탐지 기법을 고려하는 것이 좋습니다.
이 방법은 간단하고 효율적이며, Z-점수를 계산해 특정 기준을 정하여 이상치를 식별하는 방법으로, 평균 중심성과 표준편차를 이용해 수행할 수 있습니다.

# 이상치 검출
def find_and_plot_zscore_outliers(data, threshold=3):
    z_scores = (data - data.mean()) / data.std()
    outliers = data[abs(z_scores) > threshold]
    return f"Total number of outliers are {len(outliers)}"

# 시각화
fig, axis = plt.subplots(1, 2, figsize=(10, 3))

outliers_gain = find_and_plot_zscore_outliers(train['capital.gain'], threshold=3)
outliers_loss = find_and_plot_zscore_outliers(train['capital.loss'], threshold=3)

axis[0].set_title('Capital Gain Z-Score Outliers\n' + outliers_gain)
axis[1].set_title('Capital Loss Z-Score Outliers\n' + outliers_loss)

sns.histplot((train['capital.gain'] - train['capital.gain'].mean()) / train['capital.gain'].std(), ax=axis[0], kde=True, bins=30)
sns.histplot((train['capital.loss'] - train['capital.loss'].mean()) / train['capital.loss'].std(), ax=axis[1], kde=True, bins=30)

plt.tight_layout()
plt.show()

※ 결과 해석

Z-Score는 데이터 포인트가 평균으로부터 표준편차의 몇 배만큼 떨어져 있는지를 나타냅니다.

Z-Score의 절대값이 3 이상일 경우, 해당 데이터 포인트는 일반적으로 이상치로 간주됩니다.

Capital Gain
Z-Score를 사용하여 계산한 결과, "capital.gain" 변수에서 이상치의 총 개수는 32개입니다.
시각화한 히스토그램에서도 Z-Score의 절대값이 3 이상인 이상치를 확인할 수 있습니다.
Capital Loss
"capital.loss" 변수에서도 이상치가 발견되었으며, 이상치의 총 개수는 162개입니다.
"capital.gain"과 마찬가지로, 히스토그램에서 Z-Score의 절대값이 3 이상인 이상치를 확인할 수 있습니다.

이러한 이상치는 모델의 학습에 방해가 될 수 있으므로, 이상치를 제거하거나 다른 방법으로 처리하는 것이 좋습니다.
이상치를 처리하지 않으면, 모델이 이러한 이상치에 과적합될 수 있으며 이는 모델의 일반화 성능을 저하시킬 수 있습니다.

4. DBSCAN을 활용한 이상치 탐지

※ DBSCAN (Density-Based Spatial Clustering of Applications with Noise)

DBSCAN은 밀도 기반의 클러스터링 알고리즘으로, 데이터의 밀도에 따라 클러스터를 형성합니다. 이 방법은 특히 이상치(outliers)를 식별하는 데 유용하며, 클러스터의 형태나 개수를 미리 지정할 필요가 없습니다.

from sklearn.cluster import DBSCAN

# DBSCAN을 이용하여 이상치를 식별하는 코드
X_db = train[['capital.gain', 'capital.loss']].values

# DBSCAN 모델 적용
db = DBSCAN(eps=0.5, min_samples=5).fit(X_db)
labels = db.labels_

# 이상치 레이블의 개수를 출력
display(pd.Series(labels).value_counts())

# 시각화를 위한 그래프 생성
fig, ax = plt.subplots(figsize=(4,4))
colors = ['blue', 'red']

# 파란색으로 표시할 데이터: 이상치가 아닌 데이터 (labels != -1)
# 빨간색으로 표시할 데이터: 이상치 데이터 (labels == -1)
for color in colors:
    outlier_mask = labels == -1 if color == 'red' else labels != -1
    x = X_db[:, 0][outlier_mask]
    y = X_db[:, 1][outlier_mask]
    ax.plot(x, y, 'o', color=color)
    
plt.show()

※ 결과 해석

1) 시각화 해석
파란색 점 (Inliers): 이상치가 아닌 정상 데이터 포인트들을 나타냅니다.
이들은 DBSCAN 알고리즘에 의해 각각 다른 클러스터에 할당되었거나, 단일 클러스터로 그룹화되었습니다.

빨간색 점 (Outliers): 이상치로 간주되는 데이터 포인트들입니다.
이들은 어떤 클러스터에도 속하지 않으며, 데이터의 분포에서 떨어져 있음을 시각적으로 확인할 수 있습니다.

2) 레이블 개수 해석
labels를 통해 각 클러스터 및 이상치의 수를 확인할 수 있습니다.
이 값에서 -1은 이상치를 나타내며, 다른 숫자들은 각각의 클러스터를 의미합니다.

이상치 (레이블 -1): 총 196개의 이상치가 식별되었습니다.
클러스터 레이블: 가장 큰 클러스터는 레이블 0으로, 약 388개의 데이터 포인트를 포함합니다. 그 외에도 여러 작은 클러스터들이 존재합니다.

3) 결과 및 추가 고려 사항

DBSCAN은 "capital.gain"과 "capital.loss" 특성에 대해 명확한 클러스터와 이상치를 식별했습니다.

그러나 DBSCAN의 성능은 입력값(엡실론) 및 min_samples(최소 샘플 수) 매개변수에 크게 의존합니다.

이 매개변수들이 데이터의 특성에 적절하지 않게 설정되면 결과가 왜곡될 수 있습니다.
잘못된 매개변수 선택은 클러스터링 결과에 큰 영향을 미칠 수 있습니다.

이상치 제거 여부는 데이터의 전처리, 이상치 처리 전략 및 모델의 목표에 따라 달라질 수 있습니다.
따라서, 이상치를 제거하거나 조정할 때는 분석 목표에 맞춰 신중하게 판단하고, 필요에 따라 다른 접근 방법을 고려할 수 있습니다.

5. 데이터 불러오기 & 학습 데이터와 검증 데이터 분할

from sklearn.model_selection import train_test_split

train_origin = pd.read_csv('train.csv')
train_data, valid_data = train_test_split(train_origin, test_size=0.2, random_state=42, stratify=train_origin['target'])

※ stratify는 데이터 분할 시 적용할 층화 추출(stratified sampling) 옵션입니다.

층화 추출은 주어진 데이터셋을 여러 부분집합으로 나눌 때 각 부분집합에서 특정 속성(층)의 분포를 유지하려는 목적으로 사용됩니다.

stratify 매개변수를 train_origin['target']로 설정한 경우, 데이터를 분할할 때 target 열의 값을 기준으로 데이터를 층화 추출합니다.
이렇게 하면 각 부분 데이터셋에서 target 열의 값이 분포가 원본 데이터셋과 유사하게 유지됩니다.

일반적으로 분류 문제에서 사용되며, 클래스 불균형(class imbalance) 문제를 다룰 때 도움이 됩니다.
층화 추출을 사용하면 훈련 및 검증 데이터에서 각 클래스의 비율을 유지하면서 데이터를 나눌 수 있어 모델의 일반화 성능을 향상시킬 수 있습니다.

6. 랜덤포레스트를 활용한 직업(occupation) 결측치 대체

from sklearn.ensemble import RandomForestClassifier

def impute_missing_occupation(train_data):
    # 결측값이 있는 행과 결측값이 없는 행 분리
    missing_occupation = train_data[train_data['occupation'].isnull()]
    non_missing_occupation = train_data[~train_data['occupation'].isnull()]

    # 직업(occupation) 열을 카테고리로 변환 및 숫자 인코딩
    missing_occupation = missing_occupation.copy()
    non_missing_occupation = non_missing_occupation.copy()

    # 'occupation' 열을 카테고리 타입으로 변환
    non_missing_occupation['occupation'] = non_missing_occupation['occupation'].astype('category')

    # 카테고리 목록 및 매핑 생성 & 'occupation' 열을 숫자로 인코딩
    occupation_categories = non_missing_occupation['occupation'].cat.categories
    category_to_number = {category: number for number, category in enumerate(occupation_categories)}
    non_missing_occupation['occupation'] = non_missing_occupation['occupation'].map(category_to_number)

    # 랜덤 포레스트 모델을 사용한 결측값 대체
    numeric_columns = non_missing_occupation.select_dtypes(include=['int64', 'float64']).columns.tolist() + ['occupation']

    # 입력 피처(x)와 타겟(occupation)을 분리
    x_train = non_missing_occupation[numeric_columns[:-1]]
    y_train = non_missing_occupation[numeric_columns[-1]]

    x_valid = missing_occupation[numeric_columns[:-1]]

    # 랜덤 포레스트 모델 훈련
    model = RandomForestClassifier(random_state=24)
    model.fit(x_train, y_train)
    predicted_occupation = model.predict(x_valid)

    # 결측값 대체
    missing_occupation['occupation'] = predicted_occupation

    # 데이터 합치기
    train_imputed_occupation = pd.concat([non_missing_occupation, missing_occupation])

    # 카테고리 매핑 역방향 설정
    number_to_category = {num: cat for cat, num in category_to_number.items()}

    # 'occupation' 열을 카테고리로 복원
    train_imputed_occupation['occupation'] = train_imputed_occupation['occupation'].map(number_to_category)

    return train_imputed_occupation

# 함수 호출
imputed_train_occupation = impute_missing_occupation(train_data)

7. 학습 및 테스트 데이터의 결측값 대체

imputed_train_occupation 데이터프레임의 'native.country', 'workclass' 피처의 결측치와, test 데이터셋에 존재하는 결측치를 각 피처의 최빈값(가장 빈번하게 나타나는 값) 으로 대체

from sklearn.impute import SimpleImputer

def impute_missing_values(train, valid, columns_to_impute):
    imputed_train_data = train.copy()
    imputed_valid_data = valid.copy()

    imputer = SimpleImputer(strategy='most_frequent')
    imputed_train_data[columns_to_impute] = imputer.fit_transform(imputed_train_data[columns_to_impute])
    imputed_valid_data[columns_to_impute] = imputer.transform(imputed_valid_data[columns_to_impute])

    return imputed_train_data, imputed_valid_data

columns_to_impute = ['occupation', 'workclass', 'native.country']
imputed_train_data, imputed_valid_data = impute_missing_values(imputed_train_occupation, valid_data, columns_to_impute)

8. LabelEncoder를 사용한 범주형 데이터 인코딩

from sklearn.preprocessing import LabelEncoder

def Label_encoding(train_data, test_data):
    for col in train_data.columns[1:-1]: # ID, target 피처 제외
        if train_data[col].dtype == 'object':

            le = LabelEncoder()
            train_data[col] = le.fit_transform(train_data[col])

            for label in np.unique(test_data[col]):
                if label not in le.classes_:
                    le.classes_ = np.append(le.classes_, label)
            test_data[col] = le.transform(test_data[col])
    return train_data, test_data

encoded_train, encoded_valid = Label_encoding(imputed_train_data, imputed_valid_data)

9. 이상치 제거 및 z-score 변환

이제부터는 앞서 학습한 4가지 이상치 처리 방법을 활용하여 모델을 학습하고, 각 방법이 모델 성능에 미치는 영향을 탐색해보도록 하겠습니다.

Z_encoded_train = encoded_train.copy()
Z_encoded_valid = encoded_valid.copy()

# Train 데이터의 평균, 표준편차 계산
mean_train = Z_encoded_train[['capital.loss', 'capital.gain']].mean()
std_train = Z_encoded_train[['capital.loss', 'capital.gain']].std()

# Train 데이터로 Z-점수 계산
Z_encoded_train['z_score_loss'] = (Z_encoded_train['capital.loss'] - mean_train['capital.loss']) / std_train['capital.loss']
Z_encoded_train['z_score_gain'] = (Z_encoded_train['capital.gain'] - mean_train['capital.gain']) / std_train['capital.gain']

# Train 데이터에서 이상치 제거
threshold = 3
train_no_outliers = Z_encoded_train[(Z_encoded_train['z_score_loss'].abs() <= threshold) & (Z_encoded_train['z_score_gain'].abs() <= threshold)]

# Test 데이터에서도 동일한 Z-점수 변환을 적용
Z_encoded_valid['z_score_loss'] = (Z_encoded_valid['capital.loss'] - mean_train['capital.loss']) / std_train['capital.loss']
Z_encoded_valid['z_score_gain'] = (Z_encoded_valid['capital.gain'] - mean_train['capital.gain']) / std_train['capital.gain']

10. ExtraTreesClassifier 모델을 사용한 valid 데이터 예측 및 평가

# 평가 지표 함수 정의
from sklearn.metrics import f1_score

def macro_f1_score(y_true, y_pred):
    return f1_score(y_true, y_pred, average='macro')

# 독립변수 종속변수 분리
train_y = Z_encoded_train['target']
train_x = Z_encoded_train.drop(['ID','target','capital.gain','capital.loss','education'],axis = 1)

valid_y = Z_encoded_valid['target']
valid_x = Z_encoded_valid.drop(['ID','target','capital.gain','capital.loss','education'],axis = 1)

# 모델 학습/예측/평가
from sklearn.ensemble import ExtraTreesClassifier

extra = ExtraTreesClassifier(random_state=24)
extra.fit(train_x, train_y)
Z_pred = extra.predict(valid_x)
macro_f1_score(valid_y,Z_pred)

0.7696345481942674

※ 평가 지표를 Macro F1으로 설정한 이유

1) 불균형 데이터셋의 문제점

클래스 불균형: 불균형한 데이터셋에서는 한 클래스의 샘플 수가 다른 클래스보다 훨씬 많습니다.
이는 다수 클래스의 패턴은 잘 학습하지만, 소수 클래스의 패턴을 제대로 학습하지 못할 수 있습니다.

성능 평가의 어려움: 전통적인 정확도(Accuracy) 지표는 이러한 불균형 데이터를 평가할 때, 모델의 성능을 과대평가하게 만들 수 있습니다.
예를 들어, 90%가 한 클래스에 속하는 데이터셋에서, 그 클래스만 예측하는 모델도 높은 정확도를 보일 수 있습니다.

2)평가 지표의 선택 기준

정밀도 (Precision) 는 모델이 True로 예측한 것들 중 실제 True인 비율을 재현율 (Recall)은 실제 True인 것들 중 모델이 True로 올바르게 예측한 비율을 나타냅니다.

F1 Score는 정밀도와 재현율의 조화 평균으로, 두 지표를 동시에 고려합니다. 이는 한쪽으로 치우친 예측보다 균형 잡힌 예측을 중시합니다.

3) Macro F1 Score의 특징

Macro F1은 각 클래스에 대한 F1 Score를 먼저 계산한 후, 이를 평균화합니다.
이는 모든 클래스가 중요시되며, 소수 클래스의 성능도 중요합니다.

클래스 불균형에도 불구하고, 각 클래스의 성능을 고르게 평가함으로써 더 공정한 성능 평가를 가능하게하여 데이터 불균형에 강합니다.

※ 결과 해석

1) Macro F1 Score 값
이 값은 0에서 1 사이의 범위를 가지며, 1에 가까울수록 모델의 성능이 좋다는 것을 나타냅니다.
여기서 0.76은 상당히 높은 성능을 나타냅니다. 특히 불균형한 데이터셋에서 이와 같은 점수는 긍정적으로 평가될 수 있습니다.

2) 이상치 제거의 영향
Z-score를 사용하여 이상치를 제거한 후 모델을 학습시켰습니다.
이상치 제거는 모델의 성능에 긍정적인 영향을 미칠 수 있습니다.
이상치가 제거된 데이터는 모델이 더 정확히 일반적인 패턴을 학습하도록 도울 수 있습니다.

3) 데이터 전처리의 중요성
결측치 대체, 레이블 인코딩, 이상치 제거 등 전처리 단계는 모델의 성능에 중요한 영향을 미칩니다.
이 과정을 통해 데이터의 질을 향상시키고, 모델이 데이터를 더 잘 이해할 수 있게 만듭니다.

11. 로그 변환(Log1p)을 적용한 모델 훈련 및 평가

L_encoded_train = encoded_train.copy()
L_encoded_valid = encoded_valid.copy()

L_encoded_train['log1p_loss'] = np.log1p(L_encoded_train['capital.loss'])
L_encoded_train['log1p_gain'] = np.log1p(L_encoded_train['capital.gain'])

L_encoded_valid['log1p_loss'] = np.log1p(L_encoded_valid['capital.loss'])
L_encoded_valid['log1p_gain'] = np.log1p(L_encoded_valid['capital.gain'])

train_y = L_encoded_train['target']
train_x = L_encoded_train.drop(['ID','target','capital.gain','capital.loss','education'],axis = 1)

valid_y = L_encoded_valid['target']
valid_x = L_encoded_valid.drop(['ID','target','capital.gain','capital.loss','education'],axis = 1)

extra = ExtraTreesClassifier(random_state=24)
extra.fit(train_x, train_y)
L_pred = extra.predict(valid_x)
macro_f1_score(valid_y,L_pred)

0.771228613845421

※ 결과 해석

1) Macro F1 Score
로그 변환을 적용한 데이터에 대해 계산된 macro F1 score는 약 0.77로, 이는 상당히 높은 성능을 나타냅니다.
특히 불균형한 데이터셋에서 높은 점수는 모델이 각 클래스를 균등하게 잘 처리하고 있음을 나타냅니다.

2) 로그 변환 vs Z-Score 변환 성능 비교
이전에 수행한 Z-Score 변환을 적용한 데이터에 대한 macro F1 score는 약 0.76이었습니다.
로그 변환을 사용한 경우가 Z-Score 변환을 사용한 경우보다 약간 높은 점수를 얻었습니다.
이는 로그 변환 방식이 이 데이터셋에 더 적절한 이상치 처리 방법일 수 있음을 시사합니다.

3) 변환 방식의 차이

로그 변환:
로그 변환은 데이터의 스케일을 줄이고, 큰 값의 영향을 완화시키는 데 효과적입니다.
특히 금융, 경제 데이터와 같이 극단적인 값이 존재하는 경우 유용합니다.
Z-Score 변환:
Z-Score 변환은 데이터의 평균과 표준편차를 기반으로 이상치를 식별합니다.
이 방법은 데이터가 정규 분포를 따를 때 효과적입니다.

12. Box-Cox 변환을 적용한 모델 훈련 및 평가

B_encoded_train = encoded_train.copy()
B_encoded_valid = encoded_valid.copy()

# Box-Cox 변환을 적용하기 위해 offset 값을 설정
offset = 1  # 0보다 큰 값 (예: 1)으로 설정

# Train 데이터에 Box-Cox 변환 적용
train_capital_gain_boxcox, gain_lambda = stats.boxcox(B_encoded_train['capital.gain'] + offset)
train_capital_loss_boxcox, loss_lambda = stats.boxcox(B_encoded_train['capital.loss'] + offset)

# Train 데이터의 lambda 값 확인
print("Lambda for capital.gain (train):", gain_lambda)
print("Lambda for capital.loss (train):", loss_lambda)

# valid 데이터에 Train 데이터와 같은 lambda 값을 사용하여 Box-Cox 변환 적용
valid_capital_gain_boxcox = stats.boxcox(B_encoded_valid['capital.gain'] + offset, lmbda=gain_lambda)
valid_capital_loss_boxcox = stats.boxcox(B_encoded_valid['capital.loss'] + offset, lmbda=loss_lambda)

# Box-Cox 변환된 Train 데이터와 valid 데이터로 업데이트
B_encoded_train['boxcos.gain'] = train_capital_gain_boxcox
B_encoded_train['boxcos.loss'] = train_capital_loss_boxcox

B_encoded_valid['boxcos.gain'] = valid_capital_gain_boxcox
B_encoded_valid['boxcos.loss'] = valid_capital_loss_boxcox

train_y = B_encoded_train['target']
train_x = B_encoded_train.drop(['ID','target','capital.gain','capital.loss','education'],axis = 1)

valid_y = B_encoded_valid['target']
valid_x = B_encoded_valid.drop(['ID','target','capital.gain','capital.loss','education'],axis = 1)

extra = ExtraTreesClassifier(random_state=24)
extra.fit(train_x, train_y)
B_pred = extra.predict(valid_x)
macro_f1_score(valid_y,B_pred)

0.7682931375107168

※ 결과 해석

1) Macro F1 Score
Box-Cox 변환을 적용한 데이터에 대해 계산된 macro F1 score는 약 0.76으로, 이는 상당한 수준의 성능을 나타냅니다.
하지만 이전에 log1p 변환을 사용했을 때의 점수인 0.77보다는 낮습니다.

2) Box-Cox 변환 vs Log1p 변환

성능 비교:
Box-Cox 변환을 사용한 경우의 점수가 log1p 변환을 사용한 경우보다 낮게 나왔습니다.
이는 log1p 변환이 데이터에 대해 더 적절한 이상치 처리 방법일 가능성을 시사합니다.
변환 방식의 차이:
Box-Cox 변환은 데이터의 정규성을 향상시키는 데 유용하지만, 모든 유형의 데이터에 적합하지는 않을 수 있습니다.
Log1p 변환은 비교적 더 넓게 적용 가능한 방법으로, 특히 작은 값이 많은 데이터에 효과적입니다.

3) 데이터 특성에 따른 선택
데이터의 특성에 따라 적절한 이상치 처리 방법을 선택하는 것이 중요합니다.
이 경우 log1p 변환이 Box-Cox 변환보다 더 나은 성능을 보였습니다.

13. DASCAN 변환을 적용한 모델 훈련 및 평가

D_encoded_train = encoded_train.copy()
D_encoded_valid = encoded_valid.copy()

X_sample_scaled = D_encoded_train[['capital.gain', 'capital.loss']]

dbscan = DBSCAN(eps=0.5, min_samples=2)
clusters_sample = dbscan.fit_predict(X_sample_scaled)

D_encoded_train['clusters'] = clusters_sample
sample_no_outliers = D_encoded_train[D_encoded_train['clusters'] != -1]

train_y = sample_no_outliers['target']
train_x = sample_no_outliers.drop(['ID','target','education','clusters'],axis = 1)

valid_y = D_encoded_valid['target']
valid_x = D_encoded_valid.drop(['ID','target','education'],axis = 1)

extra = ExtraTreesClassifier(random_state=24)
extra.fit(train_x, train_y)
D_pred = extra.predict(valid_x)
macro_f1_score(valid_y,D_pred)

0.7790074659639877

※ 결과 해석

1) Macro F1 Score:
DBSCAN을 사용하여 이상치를 제거한 데이터셋에 대한 macro F1 score는 약 0.779로, 이는 높은 성능을 나타냅니다.
이 점수는 이전에 log1p 변환을 사용했을 때의 점수인 약 0.77과 비교하여 약간 더 높습니다.

2) DBSCAN 변환 vs Log1p 변환

성능 비교:
DBSCAN 변환을 사용한 경우의 점수가 log1p 변환을 사용한 경우보다 약간 높게 나왔습니다.
이는 DBSCAN 변환이 데이터셋의 이상치를 처리하는 데 더 적합한 방법일 가능성을 시사합니다.
변환 방식의 차이:
DBSCAN은 밀도 기반 클러스터링 알고리즘으로, 이상치를 효과적으로 식별할 수 있습니다.
Log1p 변환은 데이터 스케일을 조정하는 방법으로, 이상치의 영향을 완화하는 데 유용합니다.

3) 데이터 특성에 따른 선택
이상치 처리 방법을 선택할 때 데이터의 특성을 고려하는 것이 중요합니다.
DBSCAN은 특정 유형의 데이터에서 더 효과적일 수 있습니다.