인구 소득 예측 프로젝트 5 : 클래스 불균형(Borderline SMOTE)과 정규화(StandardScaler)를 활용한 모델 성능 최적화

qordnswnd123 2025. 1. 1. 23:39

1. 데이터 전처리 함수 정의: 범주화, 결측값 처리, 레이블 인코딩 1

import pandas as pd
import numpy as np
from sklearn.ensemble import RandomForestClassifier
from sklearn.impute import SimpleImputer
from sklearn.preprocessing import LabelEncoder

def preprocess_data(df, country_groups):
    # 교육 수준 및 결혼 상태 범주화
    df['education'].replace(['Doctorate', 'Prof-school'], 'highEducation', inplace=True)
    df['education'].replace(['Assoc-acdm', 'Assoc-voc'], 'SomeHigherEd', inplace=True)
    df['education'].replace(['Preschool', '10th', '11th', '12th', '1st-4th', '5th-6th', '7th-8th', '9th'], 'LowEducation', inplace=True)

    df['marital.status'].replace(['Never-married', 'Married-spouse-absent'], 'UnmarriedStatus', inplace=True)
    df['marital.status'].replace(['Married-AF-spouse', 'Married-civ-spouse'], 'Married', inplace=True)
    df['marital.status'].replace(['Separated', 'Divorced'], 'MarriageEnded', inplace=True)

    # 나이와 근무 시간의 결합 변수 생성
    df['age-hours'] = df['age'] * df['hours.per.week']
    df['age'] = pd.cut(np.log(df['age']), 30)

    # 국가 범주화 (훈련 데이터에서만 국가 그룹을 생성)
    for group in country_groups:
        df['native.country'].replace(country_groups[group], group, inplace=True)

    return df

def categorize_countries(df):
    country_groups = {0: [], 1: [], 2: [], 3: [], 4: []}
    for country in df['native.country'].unique():
        education_data = df[df['native.country'] == country]['target']
        proportion = sum(education_data) / education_data.count()
        
        if proportion == 0.0:
            country_groups[0].append(country)
        elif 0.0 < proportion <= 0.2:
            country_groups[1].append(country)
        elif 0.2 < proportion <= 0.4:
            country_groups[2].append(country)
        elif 0.4 < proportion <= 0.6:
            country_groups[3].append(country)
        else:
            country_groups[4].append(country)
    
    return country_groups

def impute_missing_occupation(train_data):

    missing_occupation = train_data[train_data['occupation'].isnull()] 
    non_missing_occupation = train_data[~train_data['occupation'].isnull()] # 결측값이 없는 행 

    missing_occupation = missing_occupation.copy()
    non_missing_occupation = non_missing_occupation.copy() # 원본 데이터를 손상시키지않기 위해 복사본 생성

    non_missing_occupation['occupation'] = non_missing_occupation['occupation'].astype('category') # 'occupation' 열을 카테고리 타입으로 변환
    occupation_categories = non_missing_occupation['occupation'].cat.categories # occupation 피처의 고유한 카테고리 목록을 추출
    category_to_number = {category: number for number, category in enumerate(occupation_categories)} # occupation_categories 목록의 각 카테고리에 번호를 할당한 딕셔너리를 생성
    non_missing_occupation['occupation'] = non_missing_occupation['occupation'].map(category_to_number) # 각 카테고리를 해당 번호로 인코딩

    numeric_columns = non_missing_occupation.select_dtypes(include=['int64', 'float64']).columns.tolist() + ['occupation'] # 수치형 데이터 열의 이름을 리스트 형태로 반환, 리스트에 occupation 열을 추가

    x_train = non_missing_occupation[numeric_columns[:-1]]
    y_train = non_missing_occupation[numeric_columns[-1]] # 종속변수만 선택한 후 y_train 변수에 할당
    x_valid = missing_occupation[numeric_columns[:-1]]

    model = RandomForestClassifier(random_state=24) # RandomForestClassifier 모델을 생성, random_state를 24로 설정하여 재현성을 보장
    model.fit(x_train, y_train) # 모델 학습
    predicted_occupation = model.predict(x_valid) # 모델 예측
    missing_occupation['occupation'] = predicted_occupation # 결측값 대체

    train_imputed_occupation = pd.concat([non_missing_occupation, missing_occupation]) # 결측값이 없는 데이터와 결측값을 대체한 데이터 합치기
    number_to_category = {num: cat for cat, num in category_to_number.items()} # 카테고리 매핑 역방향 설정
    train_imputed_occupation['occupation'] = train_imputed_occupation['occupation'].map(number_to_category) # 'occupation' 열을 카테고리로 복원

    return train_imputed_occupation

def impute_missing_values(train, valid, columns_to_impute):
    imputed_train_data = train.copy()
    imputed_valid_data = valid.copy()

    imputer = SimpleImputer(strategy='most_frequent')
    imputed_train_data[columns_to_impute] = imputer.fit_transform(imputed_train_data[columns_to_impute])
    imputed_valid_data[columns_to_impute] = imputer.transform(imputed_valid_data[columns_to_impute])

    return imputed_train_data, imputed_valid_data

def label_encoding(train_data, test_data):
    select_category_columns = train_data.select_dtypes(['object', 'category']).columns
    target = ['ID', 'target']  # 제외하고자 하는 열 이름
    result = [x for x in select_category_columns if x not in target]

    for col in result:
        if train_data[col].dtype == 'object' or train_data[col].dtype == 'category':
            le = LabelEncoder()
            train_data[col] = le.fit_transform(train_data[col])

            for label in np.unique(test_data[col]):
                if label not in le.classes_:
                    le.classes_ = np.append(le.classes_, label)
            test_data[col] = le.transform(test_data[col])
    return train_data, test_data

2. 데이터 전처리 함수 적용: 범주화, 결측값 처리, 레이블 인코딩 2

위에서 정의한 모든 함수들을 train 데이터셋에 적용

train_origin = pd.read_csv('train.csv')
train_data, valid_data = train_test_split(train_origin, test_size=0.2, random_state=42, stratify=train_origin['target'])

country_groups = categorize_countries(train_data)
train_origin, valid_data = preprocess_data(train_data, country_groups), preprocess_data(valid_data, country_groups)
imputed_train_occupation = impute_missing_occupation(train_origin)

columns_to_impute = ['occupation', 'workclass', 'native.country']
imputed_train_data, imputed_valid_data = impute_missing_values(imputed_train_occupation, valid_data, columns_to_impute)
encoded_train, encoded_valid = label_encoding(imputed_train_data, imputed_valid_data)

3. DBSCAN을 이용한 이상치 제거 및 데이터셋 준비

from sklearn.cluster import DBSCAN

D_encoded_train = encoded_train.copy()
D_encoded_valid = encoded_valid.copy()

X_sample_scaled = D_encoded_train[['capital.gain', 'capital.loss']]

dbscan = DBSCAN(eps=0.5, min_samples=4)
clusters_sample = dbscan.fit_predict(X_sample_scaled)

D_encoded_train['clusters'] = clusters_sample
sample_no_outliers = D_encoded_train[D_encoded_train['clusters'] != -1]

train_y = sample_no_outliers['target']
train_x = sample_no_outliers.drop(['ID','target','education.num','clusters'],axis = 1)

valid_y = D_encoded_valid['target']
valid_x = D_encoded_valid.drop(['ID','target','education.num'],axis = 1)

4. BorderlineSMOTE를 활용한 클래스 불균형 처리와 Extra Trees Classifier 교차 검증

StandardScaler 객체를 생성하고, 훈련 데이터 검증데이터에 적용합니다.
BorderlineSMOTE 객체를 생성합니다.
fit_resample 메소드를 사용하여 train_x, valid_x 데이터에 오버샘플링을 수행하고, 결과를 x_Bordersmote와 y_Bordersmote 변수에 할당합니다.
ExtraTreesClassifier를 사용하여 앙상블 학습 모델을 생성합니다.
make_scorer 함수와 f1_score를 사용하여 Macro F1 점수의 평가 지표를 생성합니다.
cross_val_score 함수를 사용하여 모델의 교차 검증을 수행합니다. 데이터를 3개의 폴드로 나누어 교차 검증을 수행합니다.
교차 검증의 평균 F1 점수를 계산하고 출력합니다.

from imblearn.over_sampling import BorderlineSMOTE
from sklearn.ensemble import ExtraTreesClassifier
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import cross_val_score
from sklearn.metrics import make_scorer, f1_score

scaler = StandardScaler()
train_x[['capital.gain', 'capital.loss','age-hours']] = scaler.fit_transform(train_x[['capital.gain', 'capital.loss','age-hours']])
valid_x[['capital.gain', 'capital.loss','age-hours']] = scaler.transform(valid_x[['capital.gain', 'capital.loss','age-hours']])

Bordersmote = BorderlineSMOTE(random_state=24)
x_Bordersmote, y_Bordersmote = Bordersmote.fit_resample(train_x, train_y)

extra = ExtraTreesClassifier(random_state=24)
f1_scorer = make_scorer(f1_score, average='macro')
cross_val_scores = cross_val_score(extra, x_Bordersmote, y_Bordersmote, cv=3, scoring=f1_scorer)

mean_f1_score = np.mean(cross_val_scores)
print("Mean Cross-Validation F1 Score:", mean_f1_score)

Mean Cross-Validation F1 Score: 0.8654758236487826

5. 데이터 특성 상호작용 시각화

result = pd.concat([train_x, train_y], axis=1)
plt.figure(figsize=(12, 6))
sns.heatmap(result.corr(), annot=True, cmap="YlGnBu")
plt.title("Relationship between Gender and Occupation (Heatmap)")
plt.show()

※ 결과 해석

1) age-hours와 hours.per.week

이 두 피처는 서로 높은 양의 상관 관계를 보입니다. 이는 age-hours가 age와 hours.per.week의 곱으로 생성된 변수이기 때문에 예상되는 결과입니다. 두 변수 모두 높은 수록, age-hours의 값도 커지기 때문입니다.

2) age-hours와 target

age-hours는 타겟 변수와도 상대적으로 높은 상관 관계를 보입니다. 이는 age-hours가 타겟 변수를 예측하는 데 중요한 정보를 가질 수 있음을 시사합니다.

3) 기타 피처들

대부분의 다른 피처들은 타겟 변수와 중간 정도 또는 약한 상관 관계를 보입니다. 이는 각 변수가 타겟 변수에 미치는 영향이 덜 명확하거나, 변수들 간의 관계가 독립적에 가까움임을 나타냅니다.

6. 모델 예측 결과 시각화: 혼동 행렬

from sklearn.model_selection import cross_val_predict
from sklearn.ensemble import ExtraTreesClassifier
from sklearn.metrics import confusion_matrix

extra = ExtraTreesClassifier(random_state=24)
binary_pred = cross_val_predict(extra, x_Bordersmote, y_Bordersmote, cv=3)

# Confusion Matrix 생성 및 시각화
cm = confusion_matrix(y_Bordersmote, binary_pred)
plt.figure(figsize=(5, 5))
plt.imshow(cm, interpolation='nearest', cmap=plt.cm.Greens)
plt.title('Confusion Matrix', size=15)
plt.colorbar()
classes = ['0 - <50k', '1 - >50k']
tick_marks = np.arange(len(classes))
plt.xticks(tick_marks, classes, rotation=45)
plt.yticks(tick_marks, classes)
plt.ylabel('True label')
plt.xlabel('Predicted label')

# Matrix 안의 숫자 출력
thresh = cm.max() / 2.
for i, j in np.ndindex(cm.shape):
    plt.text(j, i, cm[i, j], horizontalalignment="center",
             color="white" if cm[i, j] > thresh else "black")

plt.show()

※ 결과 해석

오른쪽 위 (True Negative): 2249건 - 실제 값이 0 (<50k)이고 모델이 0으로 정확하게 예측한 경우

오른쪽 위 (False Positive): 332건 - 실제 값이 0 (<50k)인데 모델이 1 (>50k)로 잘못 예측한 경우

왼쪽 아래 (False Negative): 356건 - 실제 값이 1 (>50k)인데 모델이 0으로 잘못 예측한 경우

오른쪽 아래 (True Positive): 2225건 - 실제 값이 1 (>50k)이고 모델이 1로 정확하게 예측한 경우

즉, 모델이 예측을 틀린 경우는 FP와 FN의 합계인 332 + 356 = 688건입니다. 이는 모델이 전체 데이터 중 688건을 잘못 분류했다는 것을 나타냅니다.

따라서 이 모델의 성능은 True Positive와 True Negative가 높고, False Positive와 False Negative가 상대적으로 낮아 비교적 좋다고 평가됩니다.

7. ROC 곡선을 통한 이진 분류 모델 평가

from sklearn.metrics import roc_curve, roc_auc_score

# AUC ROC를 계산하고 그래프를 그리는 함수
def calculate_and_plot_roc(y_true, y_score):
    fpr, tpr, _ = roc_curve(y_true, y_score)
    auc = roc_auc_score(y_true, y_score)

    plt.plot(fpr, tpr, color='darkorange', label=f'AUC = {auc:.2f}')
    plt.plot([0, 1], [0, 1], color='navy', linestyle='--')
    plt.xlabel('False Positive Rate')
    plt.ylabel('True Positive Rate')
    plt.title('ROC Curve')
    plt.legend(loc='lower right')
    plt.show()

    return auc

# AUC ROC를 계산하고 반환하기
auc_value = calculate_and_plot_roc(y_Bordersmote, binary_pred)

# 반환된 AUC ROC 값 출력
print(f'Returned AUC ROC Value: {auc_value}')

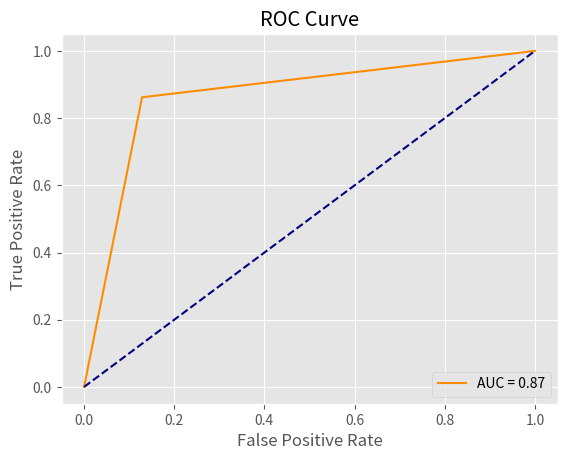
Returned AUC ROC Value: 0.8667183262301433

※ 결과 해석

AUC (Area Under the Curve)는 ROC (Receiver Operating Characteristic) 곡선 아래의 면적을 나타내는 지표로, 모델의 분류 성능을 평가하는 데 사용됩니다. ROC 곡선은 True Positive Rate (Sensitivity 또는 Recall)에 대한 False Positive Rate의 변화를 나타내며, 이 곡선 아래의 면적이 AUC입니다.

여기서 AUC 값이 0.87이라는 것은 모델이 어느 정도 좋은 성능을 보인다는 것을 의미합니다. AUC는 0과 1 사이의 값을 가지며, 1에 가까울수록 모델 성능이 우수하다고 봅니다. 보통 다음과 같이 해석됩니다:

0.5: 무작위 예측과 동일한 수준 (성능이 좋지 않음)
0.7~0.8: 어느 정도 성능이 있음
0.8~0.9: 좋은 성능
0.9 이상: 우수한 성능

따라서 AUC = 0.87은 모델이 좋은 성능을 보이고 있으며, 클래스 간의 분류를 얼마나 잘 수행하는지를 나타내는 지표입니다. ROC 곡선 아래의 면적이 상당히 넓은 편이므로, 모델이 여러 모든 경우에 높은 True Positive Rate를 유지하면서 낮은 False Positive Rate를 유지하고 있다고 해석할 수 있습니다.