아파트 경매 가격 예측 프로젝트 2 : EDA

1. 종속변수의 분포 확인

import seaborn as sns
import matplotlib.pyplot as plt

ax = sns.histplot(data=train, x="Hammer_price", bins=100)
plt.show()

 

---

2. Hammer_price(낙찰가) 와 Auction_count(총 경매 횟수)의 관계 확인

fig, ax = plt.subplots(figsize = (10,10))

x = train['Auction_count']
y = train['Hammer_price']

ax.set_xlabel('Auction_count')
ax.set_ylabel('Hammer_price')

ax.bar(x,y)
plt.show()

 

※ 결과 해석

Auction_count가 약 6회 이상일 경우 Hammer_price가 뚜렷하게 낮아지는 것이 확인됩니다.
'유찰 횟수'가 높을수록 Auction_count가 증가하는데, 일반적으로 '유찰'이 될 때마다 최저매각가격이 감소합니다.

따라서, Auction_count를 독립변수로 사용하여 Hammer_price를 예측하는 모델을 구축할 경우,
경매가 진행되면서 발생하는 유찰 횟수를 반영하고, 모델은 경매가 진행될수록 Hammer_price의 하락 경향을 학습할 수 있습니다.

---

3. Hammer_price 와 부산의 관계

train_busan = train[train['addr_do'] == '부산']

fig, ax = plt.subplots(figsize = (10,5), dpi = 100)

x = train_busan[train_busan['Hammer_price']>700000000]['addr_si'].value_counts().index
y = train_busan[train_busan['Hammer_price']>700000000]['addr_si'].value_counts().values

ax.tick_params(axis = 'x', rotation=45)
ax.bar(x,y)
plt.show()

 

---

4. Hammer_price 와 서울의 관계

train_seoul = train[train['addr_do'] == '서울']

fig, ax = plt.subplots(figsize = (10,5), dpi = 100)

x = train_seoul[train_seoul['Hammer_price']>3000000000]['addr_si'].value_counts().index
y = train_seoul[train_seoul['Hammer_price']>3000000000]['addr_si'].value_counts().values

ax.tick_params(axis = 'x', rotation=45)
ax.bar(x,y)
plt.show()

 

---

5. Auction_seq(거래 횟수) & price(가격)의 관계

fig, ax = plt.subplots(figsize = (7,5))

x_seq = result[result['Auction_key']==3]['Auction_seq']
y_min_price= result[result['Auction_key']==3]['Minimum_sales_price']
y_price= result[result['Auction_key']==3]['Appraisal_price']

ax.set_xlabel('Auction_seq')
ax.set_ylabel('Price')

ax.plot(x_seq,y_min_price)
ax.plot(x_seq,y_price)
ax.legend(['Minimum_sales_price','Appraisal_price'])
plt.show()

 

---

6. Appraisal_price(감정가) & Minimum_sales_price(최저 매각 가격)의 관계

fig, ax = plt.subplots(figsize = (10,5))

y_price_comparison = result['Appraisal_price']
y_minprice_comparison = result['Minimum_sales_price']

ax.set_xlabel('min_price_comparison')
ax.set_ylabel('price_comparisonice')

plt.xlim(0, 0.5e10)
plt.ylim(0, 0.8e10)

ax.scatter(y_minprice_comparison,y_price_comparison)
plt.show()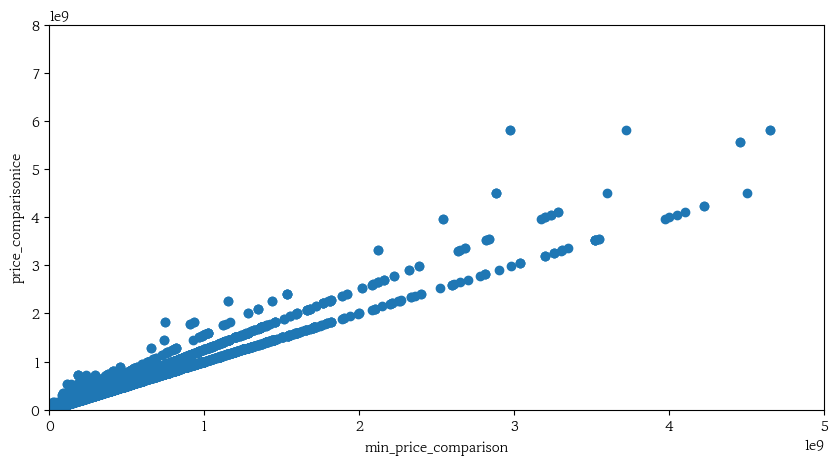

 

---

7.Total_land_auction_area(총 토지 경매 면적) & Total_land_real_area(총 토지 실면적)의 관계

fig, ax = plt.subplots(figsize = (10,5))

area = train[['Total_land_auction_area','Total_land_real_area']]

ax.scatter(x = area['Total_land_auction_area'], y = area['Total_land_real_area'])

plt.xlabel('Total_land_auction_area')
plt.ylabel('Total_land_real_area')

plt.xlim([0,250])
plt.ylim([0,250])

plt.show()

 

※ 결과 해석

경매 면적이 증가할수록 실면적도 증가합니다.
Total_land_auction_area와 Total_land_real_area는 선형관계가 나타나는 것을 보았을 때 다중공선성 관계에 해당하는 것으로 보입니다.

따라서 두 변수 중 하나의 변수를 제거함으로써 다중공선성 문제를 해결할 수 있을 것입니다.