1. 비선형성
신경망이 선형 변환만을 사용하면, 그 능력은 매우 제한적입니다. 데이터의 복잡한 패턴과 관계를 학습하기 위해서는 비선형성이 필수적인데, 이는 신경망에게 다차원 공간에서 데이터를 비틀고 구부릴 수 있는 능력을 부여합니다. CNN에서도 이 비선형성은 매우 중요한데, 합성곱 레이어의 결과에 비선형 함수를 적용하여 더욱 복잡 한 특성을 추출할 수 있게 합니다.
합성곱 후에 주로 사용되는 비선형 함수 중 하나가 ReLU(Rectified Linear Unit) 입니다. ReLU 함수는 각 픽셀 값에 대해 단순히 음수를 0으로 바꾸는 역할을 합니다. 이 작은 변화는 신경망에 큰 영향을 미치는데, 이를 통해 네트워크가 음수 데이터를 무시하고 양수에 더 중점을 둘 수 있게 되기 때문입니다.
ReLU의 적용을 통해 CNN은 입력 데이터 내의 비선형 관계를 더 잘 학습하고, 이를 특징 맵에 반영할 수 있게 돕습니다. ReLU의 적용 없이 네트워크는 선형적인 관계만을 학습하게 되어, 복잡한 패턴을 파악하는 능력이 크게 떨어질 수 있습니다. 그러므로 ReLU와 같은 비선형 활성화 함수는 CNN이 복잡한 이미지를 효과적으로 처리하고, 실제 문제에 적용될 수 있도록 하는 데에 있어 필수적인 요소입니다.
비선형성의 도입은 신경망에게 데이터 속 깊은 특징을 파고들어가 그 속에 숨겨진 더 복잡한 구조를 발견할 수 있는 '시각'을 제공합니 다. 이로 인해 CNN은 단순한 픽셀 값을 넘어서 이미지 속의 진정한 내용을 읽어낼 수 있게 됩니다.
2. 스트라이드 (Strides)
필터가 이미지의 모든 픽셀을 천천히 하나씩 탐색한다면 매우 정밀 할수는 있겠지만, 이렇게 모든 픽셀을 따라가며 특징 맵을 생성하는 일은 시간도 오래 걸리고 계산 비용도 크게 늘어납니다.
이때 등장하는 개념이 바로 스트라이드(Strides)입니다. 스트라이드는 필터가 이미지 위에서 얼마나 넓은 보폭으로 이동할 것 인지를 결정하는 중요한 매개변수입니다.
스트라이드는 필터가 이미지를 얼마나 빨리 지나가는지, 그리고 그 결과로 생성되는 특징 맵의 크기를 얼마나 줄일 것인지를 조절합니다.
스트라이드 값이 1이면 필터는 한 픽셀씩, 매우 세밀하게 이미지를 탐색합니다. 반면, 스트라이드 값을 2로 설정하면 필터는 한 번에 두 픽셀씩 건너뛰며, 이는 더 적은 양의 특징 맵을 생성하고 계산을 더 빠르게 할 수 있게 합니다.
스트라이드 값을 너무 크게 설정하면 필터가 중요한 정보를 놓치고 지나갈 위험이 있습니다. 이는 이미지의 특정 부분에서 나타나는 중요한 패턴이나 특징들이 포착되지 않을 수 있다는 의미입니다. 반대로 스트라이드가 너무 작으면 이미지의 각 부분을 너무 자세히 분석하게 되어 처리 시간이 길어집니다. 이는 신경망의 전반적인 효율성을 저하시킬 수 있습니다.
이처럼 스트라이드를 조절함으로써, 우리는 신경망의 빠른 처리 속도와 정확한 정보 추출 사이에서 최적의 균형을 찾아야 합니다. 실제 응용에서는 스트라이드 값에 따라 모델의 성능과 계산 효율 사이에서 적절한 절충안을 찾는 것이 중요합니다.
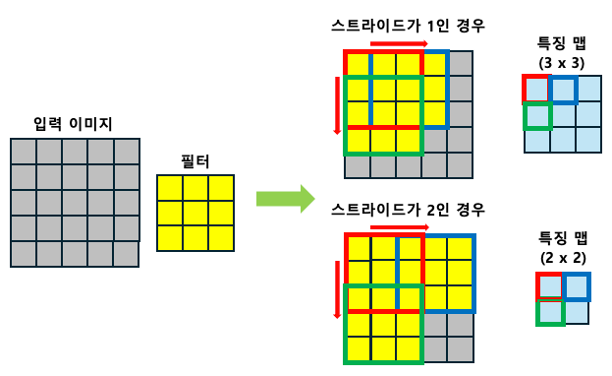
위 이미지는 스트라이드가 특징 맵(Feature Map)의 크기에 미치는 영향을 시각적으로 보여줍니다.
스트라이드가 1인 경우 필터는 매우 정밀하게 한 픽셀씩 이동하여 더 큰 특징 맵을 생성합니다. 이는 원본 이미지의 많은 정보를 포착 하지만, 계산 비용이 큽니다.
반면에 스트라이드가 2일 경우, 필터는 두 픽셀씩 건너뛰어 이동하 며, 결과적으로 더 작은 크기의 특징 맵을 생성합니다. 이는 이미지 의 일부 정보가 손실될 수 있지만, 전체적인 계산량이 감소하여 처리 속도가 빨라지는 장점이 있습니다.
3. 패딩(Padding)
필터가 이미지를 지나갈 때마다 결과물인 특징맵(Feature Map)이 점점 작아지는 문제가 발생하게 되는데 이로 인해 중요한 정보가 손실될 수 있고, 신경망의 깊이가 깊어질수록 이 문제는 더욱 심화됩니다. 입력 특징 맵의 끝 부분(모서리)에 위치한 픽셀들은 필터를 통해 충분히 활용되지 못하는 경우가 많기 때문입니다.
필터를 사용한 컨볼루션 과정에서, 입력 이미지의 크기를 유지하고 싶을때 중요한 역할을 하는 개념이 패딩(Padding)입니다.

패딩은 입력 특징 맵의 가장자리에 추가적인 픽셀(대개 0으로 채워 진)을 덧붙여 입력 특징 맵의 크기를 인위적으로 늘립니다. 이렇게 함으로써 필터가 입력 특징 맵의 모든 영역을 골고루 스캔할 수 있게 되고, 원본 이미지의 중요한 가장자리 정보도 보존할 수 있습니다.
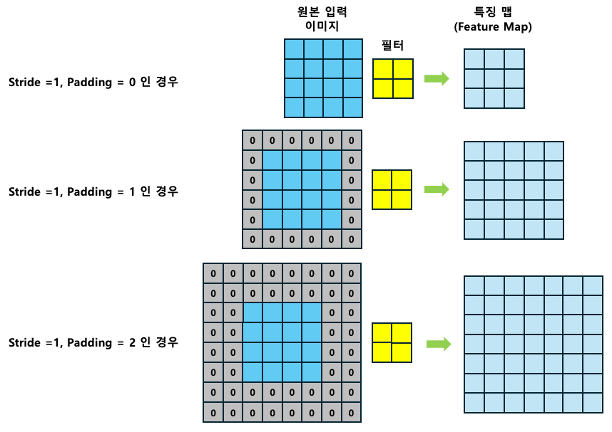
4x4 크기의 이미지에 2x2 크기의 필터를 적용 한다고 생각해 보겠습니다. 스트라이드가 1이면, 컨볼루션 후의 특징 맵은 3x3 크기로 줄어듭니다. 즉, 필터는 입력 이미지의 가장자리 부분에만 제한적으로 적용됩니다. 이는 결국 입력 이미지의 크기가 필터를 적용한 후의 특징 맵보다 줄어들게 만듭니다.
하지만, 원본 크기의 특징 맵을 원한다면 바로 패딩이 해답입니다. 패딩이 1인 경우(Stride = 1, Padding= 1)는 원본 이미지의 주위에 한 픽셀 두께의 0으로 이루어진 테두리를 추가합니다. 이렇게 하면 이미지의 크기가 5x5으로 확장됩니다. 이후 필터와 스트라이드를 적용하면, 필터는 원본 이미지의 가장자리 픽셀들도 완전히 커버할 수 있게 되며, 결과적으로 이 과정을 통 해 원본 이미지와 같은 크기의 특징 맵을 생성할 수 있습니다.
마지막으로, 패딩이 2일 때(Stride = 1, Padding = 2), 두 픽셀 두께 의 패딩이 추가됩니다. 이는 필터가 더 넓은 범위의 정보를 포함하 여 특징 맵을 생성할 수 있도록 하며, 패딩이 없을 때보다 더 큰 크기 의 특징 맵을 유지하는데 도움이 됩니다.
패딩을 사용하면 이미지의 가장자리 정보가 손실되지 않게 되며, 컨볼루션 연산을 반복할 때마다 발생하는 특징 맵의 축소를 방지할 수 있습니다. 이는 네트워크가 이미지의 중요한 시각적 정보를 보다 잘 보존하고, 학습에 더 효과적으로 사용할 수 있게 해줍니다. 이처럼 패딩은 신경망의 학습 능력을 향상시키는 데에 기여하고, 신경망이 깊어질 때 발생할 수 있는 정보 손실을 방지하는 핵심적인 요소입니다.
'딥러닝 > 딥러닝: 이미지 분류' 카테고리의 다른 글
| 데이터 증강(Data Augmentation) (0) | 2025.02.12 |
|---|---|
| PyTorch의 torchvision 패키지 (0) | 2025.02.12 |
| 평탄화 레이어(Flatten Layer)와 완전 연결 레이어(Fully Connected Layer) (0) | 2025.02.11 |
| 풀링(pooling) 기법: Max, Min, Average (0) | 2025.02.11 |
| CNN 기초 (0) | 2025.02.10 |