1. LeNet-5
LeNet-5는 사전 학습 모델은 아니지만, CNN의 기초를 이해하는 데 중요한 역할을 합니다. LeNet-5는 합성곱 신경망의 기본 개념과 구조를 명확히 보여주며, 이러한 기초가 나중에 더 복잡한 모델들, 예를 들어 AlexNet과 같은 사전 학습 모델로 발전하는 데 기여했습니다. 따라서 LeNet-5를 이해하는 것은 사전 학습 모델을 효과적으로 사용하는 데 도움이 됩니다.
손으로 쓴숫자나 문자를 컴퓨터가 어떻게 인식할 수 있을까, 또한 컴퓨터가 형태와 패턴을 구분하는 능력을 어떻게 가 지게 되었을까, 이 질문에 대한 답은 바로 합성곱 신경망(CNN)이라는 특별한 신경망 구조에 있습니다.
1.1. LeNet-5란
여러 CNN 아키텍처 중 "LeNet-5"는 심층 학습의 기초를 마련한 고전적인 모델로 널리 알려져 있습니다. 이 모델은 Yann LeCun과 그의 동료들이 1998년에 처음 발표하였으며, 주로 손으로 쓴 문자와 기계로 인쇄된 문자를 인식하는 데 사용되었습니다.
LeNet 모델이 인기를 끈 주된 이유는 단순하고 직관적인 아키텍처 때문입니다. 이는 이미지 분류를 위한 다층 합성곱 신경망입니다.
1.2. LeNet-5 아키텍처의 간략한 역사
LeNet-5는 1989년 Bell Labs에서 Yann LeCun과 그의 팀이 제안한 합성곱 신경망으로, 널리 사용되었습니다.
기존의 전통적인 방법에서는 이미지를 인식하기 위해 사람이 직접 규칙이나 템플릿을 만들어야 했습니다. 예를 들어, 손으로 쓴 숫자를 인식하기 위해서는 숫자의 모양, 선의 굵기, 곡선 등을 사람이 직접 규칙으로 정의하고 프로그램에 입력해야 했습니다. 이런 방식은 많은 시간과 노력이 필요하고, 모든 경우의 수를 커버하기 어려웠습니다.
하지만, LeNet과 같은 합성곱 신경망(CNN)은 이러한 수동적인 과정을 필요로 하지 않습니다. 대신, 신경망이 스스로 데이터를 학습하면서 특징을 추출합니다. 즉, 신경망은 훈련 데이터(예: 손으로 쓴 숫자 이미지)를 보고 각 숫자의 특징을 자동으로 학습합니다. 이렇게 하면 사람이 일일이 규칙을 정하지 않아도 컴퓨터가 스스로 학습하여 인식할 수 있게 됩니다.
따라서, LeNet은 데이터로부터 학습하고, 수동 규칙이나 템플릿에 의존하지 않고 특징을 추출할 수 있는 신경망을 개발하는 신경망입니다. 이는 신경망이 많은 양의 데이터를 통해 학습하면서 점점 더 정확하게 이미지를 인식할 수 있도록 해줍니다.
2. LeNet-5 아키텍처
LeNet-5의 아키텍처를 살펴봅시다. 이 네트워크는 학습 가능한 파라미터를 가진 5개의 레이어로 구성되어 있어 Lenet-5라고 불립니다. 이 모델에는 평균 풀링과 결합된 합성곱 층이 세 번 나오고, 그 뒤에 두 개의 완전 연결 층이 있습니다. 마지막으로, 이미지를 각 클래스에 분류하는 소프트맥스 분류기가 있습니다.

2.0) 임의의 입력 데이터 생성 (1채널, 32x32 이미지)
x = torch.randn(1, 1, 32, 32)
xtensor([[[[ 0.0719, 0.1750, -0.5917, ..., -0.5238, -0.1771, 0.0558],
[-0.5361, 0.2579, -0.1739, ..., -1.0024, -0.4934, 2.4888],
[-0.0230, -0.2815, 0.5931, ..., -1.3653, 0.3582, -0.9175],
...,
[ 0.6644, -0.8949, 1.6360, ..., 0.1766, 0.7343, 1.0632],
[-0.7534, -1.1547, -0.0523, ..., -0.6542, 0.6494, 1.8374],
[-1.2502, 0.1932, 0.9040, ..., -0.2182, 0.3382, -0.8124]]]])
※ 코드 설명
torch.randn: 이 함수는 표준 정규 분포를 따르는 랜덤한 숫자를 생성합니다. 정규 분포는 평균이 0 이고 표준편차가 1인 분포를 의미합니다.
(1, 1, 32, 32): 생성할 텐서(tensor)의 크기를 나타냅니다. 각 숫자는 해당 차원의 크기를 나타냅니다.
첫 번째 1: 배치 크기(batch size)를 의미합니다. 여기서는 배치 크기가 1이므로, 하나의 샘플을 생성합니다.
두 번째 1: 채널 수(channels)를 의미합니다. 여기서는 채널 수가 1이므로, 흑백 이미지를 나타냅니다.
세 번째 32: 이미지의 높이(height)를 의미합니다. 여기서는 32 픽셀 높이의 이미지를 생성합니다.
네 번째 32: 이미지의 너비(width)를 의미합니다. 여기서는 32 픽셀 너비의 이미지를 생성합니다.
따라서 이 코드는 1개의 배치에 1채널, 32x32 크 기의 임의의 이미지를 생성하는 코드입니다. 이 이미지는 흑백 이미지로, 각 픽셀 값은 표준 정규 분포를 따르는 랜덤 값입니다.
2.1) 첫 번째 합성곱 층 (C1)
첫 번째 합성곱 연산을 필터 크기 5X5로 적용하며, 총 6개의 필터를 사용합니다. 그 결과, 크기가 28X28X6인 특징 맵을 얻습니다. 여기서 채널 수는 적용된 필터 수와 동일합니다.

입력값이 32x32x1 크기의 이미지이고, 첫 번째 합성곱 층의 필터 크기가 5x5이며, 6개의 필터를 사용하는 경우, 합성곱 연산 과정을 다음과 같이 계산할 수 있습니다.
※ 합성곱 연산 과정
1. 입력 이미지 크기: 32x32x1 (흑백 이미지)
2. 필터 크기: 5x5
3. 필터 개수: 6개
4. 스트라이드: 기본값은 1 (명시적으로 지정되지 않은 경우)
5. 패딩: 기본값은 없음 (명시적으로 지정되지 않은 경우)
패딩이 없을 때, 출력 크기는 다음과 같이 계산됩니다.

입력 이미지의 크기가 32x32이고, 필터의 크기가 5x5, 스트라이드가 1인 경우, 출력 크기는 다음과 같이 계산됩니다.

따라서, 각 필터는 28x28 크기의 출력 특징 맵을 생성합니다.
6개의 필터를 사용하므로, 출력 특징 맵의 깊이는 6이 됩니다. 따라서 최종 출력 크기는 다음과 같습니다.
28 x 28 x 6
첫 번째 합성곱 연산은 입력 이미지에 대해 수행되며 (크기 5*5의 6개의 합성곱 커널을 사용하여) 6개의 C1 특징 맵(크기 28*28의 6개 의 특징 맵)을 얻습니다. 합성곱 커널의 크기는 5* 5이고, 총 6개의 필터가 있으므로 (5*5+ 1)* 6 = 156개의 파라미터가 필요합니다. 여기서 +1은 커널에 바이어스가 있음을 나타냅니다.
채널 수는 그대로 유지됩니다.
conv1 = nn.Conv2d(1, 6, kernel_size=5)
x = torch.tanh(conv1(x))
print(x.shape)torch.Size([1, 6, 28, 28])
※ 코드 설명
첫 번째 Convolutional 레이어를 정의하고, 이를 통해 입력 데이터를 처리한 후, 결과 텐서의 모양을 출력하는 과정입니다.
conv1 = nn.Conv2d(1, 6, kernel_size=5)
1) 첫 번째 Convolutional 레이어 정의
nn.Conv2d: 2D Convolutional 레이어를 정의하는 PyTorch 모듈입니다.
1: 입력 채널 수를 나타냅니다. 여기서는 입력 이미지가 1채널(흑백 이미지)입니다.
6: 출력 채널 수를 나타냅니다. 이 레이어는 6개의 필터(커널)를 사용하여 입력 이미지를 변환하므로, 출력 텐서는 6채널이 됩니다.
kernel_size=5: 커널의 크기를 나타냅니다. 여기서는 5x5 크기의 커널을 사용합니다.
x = torch.tanh(conv1(x))
print(x.shape)
2) Convolutional 레이어를 통한 입력 데이터 처리
convl(x): 입력 텐서 x를 첫 번째 Convolutional 레이어에 통과시킵니다. 이 과정에서 5x5 커널을 사용하여 입력 이미지의 각 위치에 대 해 합성곱 연산을 수행합니다.
torch.tanh(...): Convolutional 레이어의 출력을 하이퍼볼릭 탄젠트 함수(tanh)를 사용하여 비선형 활성화 함수를 적용합니다. tanh 함수는 입력 값을 -1에서 1 사이로 변환합니다.
print(x.shape): 처리된 텐서의 크기를 출력합니다.
입력 텐서 x의 초기 크기는 (1, 1, 32, 32)입니다. 이 텐서는 배치 크기 1, 채널 수 1, 32x32 크기의 이미지를 의미합니다. Convolutional 레이어를 통과한 후 출력 텐서의 크기는 (1, 6, 28, 28)이 됩니다. 이는 배치 크기 1, 채널 수 6, 28x28 크기의 이미지 6장을 의미합니다.
2.2) 첫 번째 풀링 층 (S2)
첫 번째 합성곱 층(C1) 이후에는 풀링 층이 있습니다. 이 풀링 층에서는 평균 풀링(average pooling)을 사용하여 입력 데이터의 크기를 줄입니다.

※ 풀링 연산 과정
입력 특징 맵 크기: 28x28x6 (첫 번째 합성곱 층의 출력)
풀링 크기: 2x2
스트라이드: 2
풀링 층에서는 각 2x2 영역의 평균 값을 계산하여 출력 특징 맵을 생성합니다. 스트라이드가 2이므로 출력 크기는 다음과 같이 계산됩니 다.

따라서 출력 특징 맵의 크기는 다음과 같습니다.
14x14x6
pool = nn.AvgPool2d(kernel_size=2, stride=2)
x = pool(x)
print(x.shape)torch.Size([1, 6, 14, 14])
※ 코드 설명
첫 번째 Pooling 레이어를 정의하고, 이를 통해 데이터를 처리한 후 결과 텐서의 모양을 출력하는 과정입니다.
# 첫 번째 pooling 레이어 정의
pool = nn.AvgPool2d(kernel_size=2, stride=2)
1) 첫 번째 Pooling 레이어 정의
nn.AvgPool2d 2D 평균 풀링 레이어를 정의하는 PyTorch 모듈입니다.
kernel_size=2 풀링 커널의 크기를 2x2로 설정합니다.
atride-2 풀링 연산의 스트라이드를 2로 설정합니다. 즉, 풀링 창이 2칸씩 이동하면서 연산을 수행합니다.
#첫 번째 pooling 레이어 통과
x = pool(x)
print(x.shape)
2) Pooling 레이어를 통한 데이터 처리
pool(x): 입력 텐서 x를 첫 번째 Pooling 레이어에 통과시킵니다. 이 과정에서 2x2 커널을 사용하여 입력 데이터의 각 위치에 대해 평균 풀링 연산을 수행합니다. 이는 각 2x2 영역 내의 값들의 평균을 계산하여 출력합니다.
print(x.shape): 풀링 레이어를 통과한 후의 텐서 크기를 출력합니다.
입력 텐서 x의 초기 크기는 (1. 6. 28. 28)입니다. 이는 배치 크기 1, 채널 수 6, 28x28 크기의 이미지를 의미합니다. 평균 풀링 레이어를 통과한 후, 출력 텐서의 크기는 (1. 6. 14. 14)이 됩니다. 이는 배치 크기 1, 채널 수 6, 14x14 크기의 이미지 6장을 의미합니다.
풀링 연산은 채널 수를 변경하지 않습니다. 따라서 여전히 6입니다.
2.3) 두 번째 합성곱 층 (C3)
두 번째 합성곱 층에서는 첫 번째 풀링 층의 출력을 입력으로 받아 더 깊은 특징을 추출합니다.

※ 합성곱 연산 과정
1) 입력 특징 맵 크기: 14x14x6 (첫 번째 풀링 층의 출력)
2) 필터 크기: 5x5
3) 필터 개수: 16개
4) 스트라이드: 기본값은 1 (명시적으로 지정되지 않은 경우)
5) 패딩: 기본값은 없음 (명시적으로 지정되지 않은 경우)
패딩이 없을 때, 출력 크기는 다음과 같이 계산됩니다.

따라서, 각 필터는 10x10 크기의 출력 특징 맵을 생성합니다.
16개의 필터를 사용하므로, 출력 특징 맵의 깊이는 16이 됩니다. 따라서 최종 출력 크기는 다음과 같습니다.
10 x 10 x 16
두 번째 합성곱 층의 경우, 각 필터는 5x5 크기로 16개의 필터를 사용하므로 (5*5+1)* 16=416개의 파라미터가 필요합니다. 여기서 +1은 커널에 바이어스가 있음을 나타냅니다.
conv2 = nn.Conv2d(6, 16, kernel_size=5)
x = torch.tanh(conv2(x))
print(x.shape)torch.Size([1, 16, 10, 10])
※ 코드 설명
두 번째 Convolutional 레이어를 정의하고, 이를 통해 데이터를 처리한 후 결과 텐서의 모양을 출력하는 과정입니다.
conv2 = nn.conv2d(6, 16, kernel_size=5)
1) 두 번째 Convolutional 레이어 정의
입력 채널 수를 나타냅니다. 여기서는 이전 레이어의 출력이 6채널이므로, 입력 채널 수는 6입니다.
16 출력 채널 수를 나타냅니다. 이 레이어는 16개의 필터(커널)를 사용하여 입력 이미지를 변환하므로, 출력 텐서는 16채널이 됩니다.
kernel_size=5:5x5 크기의 커널을 사용합니다.
x = torch.tanh(conv2(x))
print(x.shape)
2) Convolutional 레이어를 통한 데이터 처리
conv2(x): 입력 텐서 x를 두 번째 Convolutional 레이어에 통과시킵니다. 이 과정에서 5x5 커널을 사용하여 입력 이미지의 각 위치에 대 해 합성곱 연산을 수행합니다.
toroh_tanh(...): Convolutional 레이어의 출력을 하이퍼볼릭 탄젠트 함수(tanh)를 사용하여 비선형 활성화 함수를 적용합니다.
print(x.ahape): 처리된 텐서의 크기를 출력합니다.
입력 텐서 x의 초기 크기는 (1. 6. 14. 14)입니다. 이는 배치 크기 1, 채널 수 6, 14x14 크기의 이미지를 의미합니다. Convolutional 레이 어를 통과한 후, 출력 텐서의 크기는 (1. 16. 10. 10)이 됩니다. 이는 배치 크기 1, 채널 수 16, 10x10 크기의 이미지 16장을 의미합니다.
2.4) 두 번째 풀링 층 (S4)
두번째 항성곱 층 이휴에는 두번째 풀링층이 있습니다. 이 풀링 층에서는 첫번쨰 풀링층과 동일하게 평균 풀링을 사용합니다.
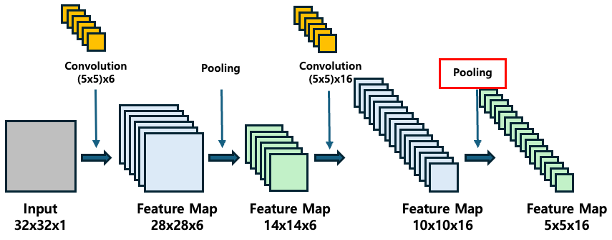
※ 풀링 연산 과정
1) 입력 특징 맵 크기: 10x10x16 (두 번째 합성곱 층의 출력)
2) 풀링 크기: 2x2
3) 스트라이드: 2
풀링 층에서는 각 2x2 영역의 평균 값을 계산하여 출력 특징 맵을 생성합니다. 스트라이드가 2이므로 출력 크기는 다음과 같이 계산됩니 다.

따라서 출력 특징 맵의 크기는 다음과 같습니다.
5x5x16
x = pool(x)
print(x.shape)torch.Size([1, 16, 5, 5])
※ 코드 설명
앞서 정의된 풀링 레이어를 사용하여 데이터를 처리한 후, 결과 텐서의 모양을 출력하는 과정을 보여줍니다.
x = pool(x)
print(x.shape)
1) Pooling 레이어를 통한 데이터 처리
pool(x): 이전에 정의된 풀링 레이어 (pool = nn.AvgPool2d(kernel_size=2. stride-2))를 사용하여 입력 텐서 x를 처리합니다. 이 풀링 레이어는 평균 풀링(Average Pooling) 연산을 수행합니다.
print(x.ahape): 풀링 레이어를 통과한 후의 텐서 크기를 출력합니다.
입력 텐서 x의 초기 크기는 (1. 16. 10. 10)입니다. 이는 배치 크기 1, 채널 수 16, 10x10 크기의 이미지를 의미합니다. 평균 풀링 레이어를 통과한 후, 출력 텐서의 크기는 (1. 16. 5. 5)이 됩니다. 이는 배치 크기 1, 채널 수 16, 5x5 크기의 이미지 16장을 의미합니다.
2.5) 세 번째 합성곱 층 (C5)
세 번째 합성곱 층에서는 두 번째 풀링 층의 출력을 입력으로 받아 더 깊은 특징을 추출합니다.

※ 합성곱 연산 과정
1) 입력 특징 맵 크기: 5x5x16 (두 번째 풀링 층의 출력)
2) 필터 크기: 5x5
3) 필터 개수: 120개
4) 스트라이드: 기본값은 1 (명시적으로 지정되지 않은 경우)
5) 패딩: 기본값은 없음 (명시적으로 지정되지 않은 경우)
패딩이 없을 때, 출력 크기는 다음과 같이 계산됩니다.

따라서, 각 필터는 1x1 크기의 출력 특징 맵을 생성합니다.
120개의 필터를 사용하므로, 출력 특징 맵의 깊이는 120이 됩니다. 따라서 최종 출력 크기는 다음과 같습니다.
1x1x120
세 번째 합성곱 층의 경우, 각 필터는 5x5 크기로 120개의 필터를 사용하므로 (5*5+ 1)* 120 = 3,120개의 파라미터가 필요합니다. 여기서 +1은 커널에 바이어스가 있음을 나타냅니다.
conv3 = nn.Conv2d(16, 120, kernel_size=5)
x = torch.tanh(conv3(x))
print(x.shape)torch.Size([1, 120, 1, 1])
2.6) 완전 연결층 (FC1)
완전 연결층(Fully Connected Layer)은 합성곱 층과 풀링 층에서 추출된 특징을 바탕으로 최종 분류를 수행하는 역할을 합니다. LeNet-5에서는 두 개의 완전 연결층이 있습니다.
완전 연결층은 세 번째 합성곱 층의 출력을 평탄화 (flattening)하여 1차원 벡터로 변환한 후, 이를 입력으로 받아 분류 작업을 수행합니다.

※ 완전 연결층 연산 과정
1) 입력 특징 맵 크기: 1x1x120 (세 번째 합성곱 층의 출력)
2) 평탄화: 입력을 1차원 벡터로 변환
1x1x120 -> 120
3) 완전 연결층 (F6)
뉴런 수:84
학습 가능한 파라미터: (120+1)*84
각 뉴런은 120개의 입력을 가지며, 각 입력에 대해 가중치가 존재합니다.
또한 각 뉴런은 바이어스 값을 가집니다.
따라서 총 학습 가능한 파라미터 수는 (120*84) + 84 = 10,164개입니다.
# Flatten (벡터로 변환)
x_flatten = x.view(-1, 120)
print(x_flatten.shape)
# 첫 번째 Fully Connected 레이어 정의
fc1 = nn.Linear(120, 84)
# 첫 번째 Fully Connected 레이어 통과
x = torch.tanh(fc1(x_flatten))
print(x.shape)torch.Size([1, 120])
torch.Size([1, 84])
※ 코드 설명
Convolutional 레이어의 출력을 평탄화(Flatten)하고, 이를 Fully Connected (또는 Dense) 레이어에 통과시킨 후 결과 텐서의 모양을 출력하는 과정입니다.
# Flatten (벡터로 변환)
x = x.view(-1, 120)
print(x.shape)
1) Flatten (벡터로 변환):
x_view(-1, 120): 이 코드는 텐서 x의 크기를 변경하여 평탄화(Flatten)합니다. view 메소드는 텐서의 크기를 변경하는데 사용됩니다.
-1: PyTorch가 자동으로 배치 크기를 계산하도록 합니다.
120: 각 샘플의 피쳐(특징) 수입니다. 이 값은 이전 Convolutional 레이어의 출력 채널 수입니다.
print(x.ahape): 변환된 텐서의 크기를 출력합니다.
입력 텐서 x의 초기 크기는 (1. 120. 1. 1)이었습니다. view 메소드를 사용하여 (1. 120) 형태로 평탄화하므로, 출력 텐서의 크기는 (1. 120)이 됩니다. 이는 배치 크기 1과 피쳐 수 120을 의미합니다.
# 첫 번째 Fully connected 레이어 정의
fc1= nn.Linear(120, 84)
2) 첫 번째 Fully Connected 레이어 정의:
nn.Linear(120.84): Fully Connected 레이어를 정의합니다.
120: 입력 피쳐 수입니다. 이는 평탄화된 입력의 크기와 일치합니다.
84: 출력 피쳐 수입니다. 이 레이어는 84개의 뉴런을 사용하여 입력 데이터를 변환합니다.
#첫 번째 Fully connected 레이어 통과
x = torch.tanh(fc1(x))
print(x.shape)
3) Fully Connected 레이어를 통한 데이터 처리:
fo1(x): 평탄화된 입력 텐서 x를 첫 번째 Fully Connected 레이어에 통과시킵니다. 이 레이어는 입력 데이터에 선형 변환을 적용합니다.
toroh.tanh(...): Fully Connected 레이어의 출력을 하이퍼볼릭 탄젠트 함수(tanh)를 사용하여 비선형 활성화 함수를 적용합니다.
print(x.ahape): 처리된 텐서의 크기를 출력합니다.
평탄화된 입력 텐서 x의 크기는 (1. 120)이었습니다. 첫 번째 Fully Connected 레이어를 통과한 후, 출력 텐서의 크기는 (1. 84)이 됩니다. 이는 배치 크기 1 과 피쳐 수 84를 의미합니다.
2.7) 출력층(FC2)
출력층은 최종 분류를 수행하는 층으로, LeNet-5에서는 10개의 클래스로 분류하기 위해 10개의 뉴런을 가지고 있습니다. 소프트맥스 활성화 함수를 사용하여 각 클래스에 대한 확률을 계산합니다.

※ 출력층 연산 과정
1) 입력 특징 벡터 크기: 84 (완전 연결층 F6의 출력)
2) 출력층 (Output Layer)
뉴런 수: 10 (분류할 클래스 수)
학습 가능한 파라미터: (84+ 1)* 10
각 뉴런은 84개의 입력을 가지며, 각 입력에 대해 가중치가 존재합니다.
또한 각 뉴런은 바이어스 값을 가집니다.
따라서 총 학습 가능한 파라미터 수는 (84*10)+10=850개입니다.
최종 분류 과정
출력층에서는 소프트맥스(softmax) 활성화 함수를 사용하여 각 클래스에 대한 확률을 계산합니다. 소프트맥스 함수는 입력 값을 정규화하여 각 클래스가 선택될 확률을 반환합니다. 가장 높은 확률을 가진 클래스가 최종 예측 값이 됩니다.
fc2 = nn.Linear(84, 10)
x = fc2(x)
print(x.shape)torch.Size([1, 10])
※ 코드 설명
두 번째 Fully Connected (또는 Dense) 레이어를 정의하고, 이를 통해 데이터를 처리한 후 결과 텐서의 모양을 출력하는 과정입니다.
# 두 번째 Fully connected 레이어 정의
fc2 = nn.Linear(84, 10)
1) 두 번째 Fully Connected 레이어 정의:
nn.Linear (84, 10): Fully Connected 레이어를 정의합니다.
84: 입력 피쳐 수입니다. 이는 첫 번째 Fully Connected 레이어의 출력 피쳐 수와 일치합니다.
10: 출력 피쳐 수입니다. 이 레이어는 10개의 뉴런을 사용하여 입력 데이터를 변환합니다. 일반적으로 이는 10개의 클래스로 분류하는 문제에서 사용됩니다.
# 두 번째 Fully connected 레이어 통과
x=fc2(x) print(x.shape)
2) Fully Connected 레이어를 통한 데이터 처리:
fo2(x): 첫 번째 Fully Connected 레이어의 출력을 두 번째 Fully Connected 레이어에 통과시킵니다. 이 레이어는 입력 데이터에 선형 변환을 적용합니다.
print(x.ahape): 처리된 텐서의 크기를 출력합니다.
입력 텐서 x의 초기 크기는 (1.84)이었습니다. 두 번째 Fully Connected 레이어를 통과한 후, 출력 텐서의 크기는 (1. 10)이 됩니다. 이는 배치 크기 1과 피쳐 수 10을 의미합니다. 출력 피쳐 수 10 은 일반적으로 10개의 클래스로 구성된 분류 문제에서 각 클래스에 대한 점수 또는 확률을 나타냅니다.
요약하면, 이 코드는 첫 번째 Fully Connected 레이어의 출력을 두 번째 Fully Connected 레이어에 통과시켜 최종적으로 10개의 클래스로 데이터를 변환하는 과정을 보여줍니다. 이 과정은 주로 이미지 분류와 같은 작업에서 사용되며, 최종 레이어의 출력은 각 클래스에 대한 로짓(logits) 또는 점수로 해석될 수 있습니다. 최종 예측을 위해서는 이 출력에 소프트맥스(softmax) 함수를 적용 하여 각 클래스에 대한 확률을 계산할 수 있습니다.
3. LeNet-5 모델 클래스 정의
※ LeNet-5 아키텍처 요약
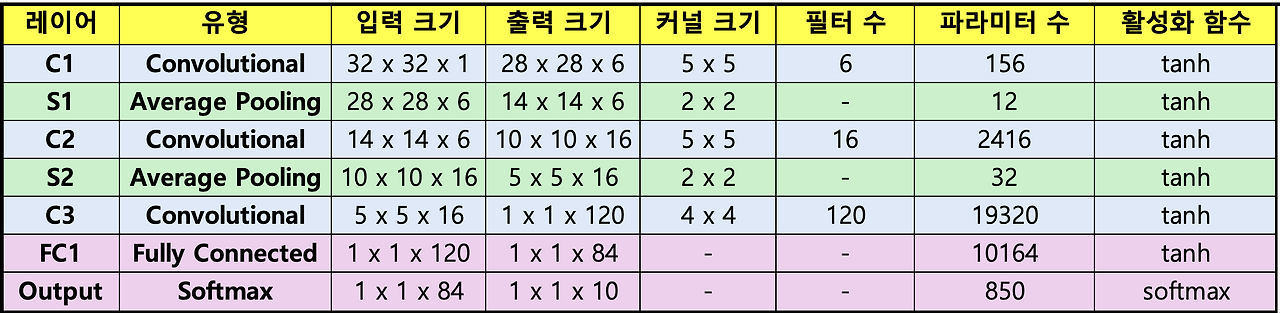
- 이 모델의 입력은 32X32 크기의 그레이스케일 이미지로, 채널 수는 하나입니다.
- 다음은 5X5 크기의 6개 필터와 스트라이드 1을 가진 첫 번째 합성곱 층입니다. 이 층에서 사용되는 활성화 함수는 tanh입니다. 출력 특징 맵은 28X28X6입니다.
- 그 다음은 필터 크기 2X2와 스트라이드 1을 가진 평균 풀링 층입니다. 결과적인 특징 맵은 14X14X6입니다. 풀링 층은 채널 수에 영향을 주지 않습니다.
- 그 후, 5X5 크기의 16개 필터와 스트라이드 1을 가진 두 번째 합성곱 층이 있습니다. 활성화 함수는 tanh입니다. 이제 출력 크기는 10X10X16입니다.
- 다시 필터 크기 2X2와 스트라이드2를 가진 또 다른 평균 풀링 층이 있습니다. 결과적으로 특징 맵 크기는 5X5X16으로 줄어듭니다.
- 최종 풀링 층은 5X5 크기의 120개 필터와 스트라이드 1을 가지며, 활성화 함수는 tanh입니다. 출력 크기는 120입니다.
- 다음은 84개의 뉴런을 가진 완전 연결 층으로, 출력은 84개의 값이 되며, 활성화 함수는 tanh입니다.
- 마지막 층은 10개의 뉴런과 소프트맥스 함수로 구성된 출력 층입니다. 소프트맥스는 데이터 포인트가 특정 클래스에 속할 확률을 제공합니다. 가장 높은 값이 예측값이 됩니다.
※ LeNet-5의 특징
합성곱, 풀링, 비선형 활성화 함수로 구성된 합성곱 레이어: LeNet-5의 모든 합성곱 레이어는 이 세 가지 부분으로 구성되어 있습니다. 합성곱 레이어는 이미지의 공간적 특성을 추출하는 역할을 합니다.
공간적 특성 추출을 위한 합성곱 합성곱 레이어는 입력 이미지의 공간적 특성을 추출합니다. 이는 원래 '수용 필드'라고 불리며, 각 뉴런이 입력 이미지의 특정 영역을 인식하는 방식입니다.
서브샘플링에 사용되는 평균 풀링 층: LeNet-5는 평균 풀링 층을 사용하여 특징 맵의 크기를 줄입니다. 이는 다운샘플링 과정을 통해 계산 복잡성을 줄이고, 중요한 특징을 추출하는 데 도움이 됩 니다.
활성화 함수로 사용되는 tanh: LeNet-5는 활성화 함수로 tanh'를 사용합니다. 이는 비선형성을 도입하여 신경망이 더 복잡한 패턴을 학습할 수 있도록 합니다.
다층 퍼셉트론 또는 완전 연결 레이어를 사용한 마지막 분류기: LeNet-5의 마지막에는 다층 퍼셉트론 또는 완전 연결 레이어가 위치하며, 이 레이어는 추출된 특징을 바탕으로 최종 분류를 수행합 니다.
3.1) 클래스로 구현한 AlexNet 모델
class LeNet5(nn.Module):
def __init__(self):
super(LeNet5, self).__init__()
self.conv1 = nn.Conv2d(1, 6, kernel_size=5)
self.pool = nn.AvgPool2d(kernel_size=2, stride=2)
self.conv2 = nn.Conv2d(6, 16, kernel_size=5)
self.conv3 = nn.Conv2d(16, 120, kernel_size=5)
self.fc1 = nn.Linear(120, 84)
self.fc2 = nn.Linear(84, 10)
def forward(self, x):
x = torch.tanh(self.conv1(x))
x = self.pool(x)
x = torch.tanh(self.conv2(x))
x = self.pool(x)
x = torch.tanh(self.conv3(x))
x = x.view(-1, 120)
x = torch.tanh(self.fc1(x))
x = self.fc2(x)
return x
3.2) LeNet-5 모델 생성 및 요약 정보 출력
model = LeNet5()
summary(model, (1, 32, 32))----------------------------------------------------------------
Layer (type) Output Shape Param #
================================================================
Conv2d-1 [-1, 6, 28, 28] 156
AvgPool2d-2 [-1, 6, 14, 14] 0
Conv2d-3 [-1, 16, 10, 10] 2,416
AvgPool2d-4 [-1, 16, 5, 5] 0
Conv2d-5 [-1, 120, 1, 1] 48,120
Linear-6 [-1, 84] 10,164
Linear-7 [-1, 10] 850
================================================================
Total params: 61,706
Trainable params: 61,706
Non-trainable params: 0
----------------------------------------------------------------
Input size (MB): 0.00
Forward/backward pass size (MB): 0.06
Params size (MB): 0.24
Estimated Total Size (MB): 0.30
----------------------------------------------------------------
3.3) 입력 데이터 생성 및 손실 계산
# 입력 데이터 생성
x = torch.randn(1, 1, 32, 32)
# 순전파
logits = model(x)
print(logits.shape) # (1, 10)
# 손실 함수 정의 및 사용
criterion = nn.CrossEntropyLoss()
target = torch.tensor([1]) # 예시 정답 레이블
loss = criterion(logits, target)
print(loss)torch.Size([1, 10])
tensor(2.3484, grad_fn=<NllLossBackward0>)'딥러닝 > 딥러닝: 자연어 처리' 카테고리의 다른 글
| 임베딩(Embedding) (0) | 2025.02.25 |
|---|---|
| AlexNet (2012) (0) | 2025.02.25 |
| 토크나이저 (0) | 2025.02.19 |
| 자연어 데이터 전처리 (0) | 2025.02.13 |
| 자연어 처리 개요 (1) | 2025.02.13 |