회귀분석
회귀분석은 우리가 변수들 사이의 관계를 이해하고 예측하는 데 도움을 주는 통계적 방법입니다.
간단히 말해서, 이 방법은 하나의 변수(우리가 예측하고 싶은 것, 종속 변수)가 다른 변수들(독립 변수)에 의해 어떻게 영향을 받는지를 알려줍니다.
※ 회귀분석의 종류
- 단순 선형 회귀
하나의 독립 변수와 하나의 종속 변수 사이의 관계를 알려줍니다. - 다중 선형 회귀
여러 독립 변수(예: 광고 지출, 시장 규모, 계절 등)를 사용하여 종속 변수를 예측합니다. - 로지스틱 회귀
예/아니오와 같은 범주형 종속 변수를 예측할 때 사용됩니다.
※ 회귀분석의 장점
- 작은 데이터 세트에서도 효과적
회귀분석은 거대한 데이터가 없어도 잘 작동합니다. 큰 데이터 세트를 필요로 하는 복잡한 머신러닝 모델과 달리, 회귀모델은 상대적으로 작은 데이터로도 의미 있는 결과를 줄 수 있습니다. - 간단하고 비용이 적게 드는 모델
회귀모델은 복잡하지 않습니다. 그래서 컴퓨터가 이해하고 계산하기에 부담이 적습니다. 빠른 모델 훈련과 예측이 필요할 때 좋습니다. 시간과 자원을 아낄 수 있습니다. - 이해와 설명이 중요할 때
예측의 정확성만큼 중요한 것이 데이터의 패턴을 이해하고 설명하는 것이라면, 회귀분석이 적합합니다. 이 방법은 데이터가 어떻게 움직이는지, 왜 그런지를 보여줍니다. - 선형 관계가 강한 데이터에 적합
만약 데이터가 선형적인 패턴을 보인다면, 회귀분석은 높은 정확도를 제공할 수 있습니다. 즉, 하나의 변수가 변할 때 다른 변수도 예측 가능한 방식으로 변하는 데이터에 적합합니다.
※ 한계점
- 선형 관계에만 집중
회귀 모델은 변수들 사이에 직선 같은 선형 관계가 있다고 가정합니다. 따라서 산이나 곡선처럼 구부러진 비선형 관계를 가진 데이터에는 회귀분석이 잘 맞지 않을 수 있습니다. - 단순함의 한계
회귀분석은 비교적 간단한 모델입니다. 이 단순함은 이해하기 쉽고 계산하기 편하게 만들어 주지만, 때로는 데이터의 복잡한 패턴이나 관계를 완전히 포착하거나 설명하기에는 부족할 수 있습니다.
1. 단순선형 회귀분석 (Simple Linear Regression)
선형 회귀분석에서의 주요 구성요소는 아래와 같습니다.
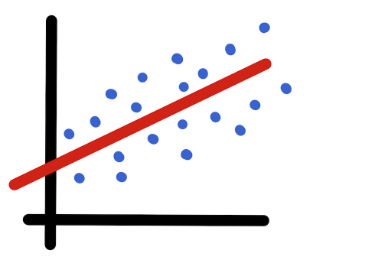
- 독립 변수 (Independent Variable)
이것은 우리가 예측하거나 설명하고자 하는 변수입니다. - 종속 변수 (Dependent Variable)
이것은 우리가 예측하려는 변수로, 독립 변수에 의해 영향을 받습니다. - 회귀선 (Regression Line)
이 선은 데이터 포인트들 사이의 관계를 나타냅니다. 가장 잘 맞는, 즉 '최적'의 선형 관계를 표현하는 선입니다. 이 선을 통해 우리는 독립 변수가 변할 때 종속 변수가 어떻게 변할지 예측할 수 있습니다.
단순 회귀분석은 한 개의 독립 변수와 한 개의 종속 변수를 가지는 선형 관계를 모델링합니다.
단순 회귀분석 식은 아래와 같습니다.
a+bX+ϵ
- X: 독립변수(independent variables)
- Y: 종속변수(dependent variable), 이 변수의 값은 다른 변수에 의해 영향을 받습니다.
- a: 회귀 계수, y 절편(intercept) 이라고 하며, 독립변수 X값이 0일 때 Y의 예상 값입니다.
- b: 회귀 계수, 기울기(slop)이며, 독립변수 X가 한 단위 변할 때 종속변수 Y가 얼마나 변하는지를 나타냅니다.
- ϵ: 오차(Error) 항으로, 모델이 설명하지 못하는 무작위 변동성을 나타냅니다.
회귀 계수를 구하는 방법은 최소제곱법(OLS)를 이용합니다.
구체적인 순서는 아래와 같습니다.
- 회귀 모델 정의
- 오차의 제곱합 계산: 여러 독립 변수에 대해 실제 값과 회귀 모델에 의해 예측된 값 사이의 차이의 제곱합을 계산합니다.
- 제곱합 최소화: 이를 최소화하는 절편과 각 독립 변수에 대한 회귀계수 값을 찾습니다.
2. 다중선형 회귀분석(Multiple Linear Regression)
다중 회귀분석은 여러개의 독립 변수와 한 개의 종속 변수를 가지는 선형 관계를 모델링합니다.
다중 회귀분석 식은 아래와 같습니다.
회귀 식의 해석
회귀 식을 통해 데이터에서 관찰되는 관계의 강도와 방향을 이해할 수 있습니다.
예를 들어, 기울기 b의 값이 양수이면 X와 Y가 양의 관계를 가진다는 것을 의미하며, 값이 클수록 관계가 강해집니다.
반대로, b가 음수이면 음의 관계를 나타냅니다.
회귀 식은 또한 예측 목적으로 사용됩니다.
독립 변수 X의 새로운 값을 식에 대입하여, 해당하는 종속 변수 Y의 예상 값을 계산할 수 있습니다.
3. 회귀분석 기본가정
이러한 가정들은 회귀 모델을 적용하기 전에 검토하고, 필요한 경우 조정하거나 다른 분석 방법을 고려해야 합니다.
데이터가 이러한 가정을 충족하지 않을 경우, 변환을 적용하거나 다른 종류의 회귀 모델을 사용하는 것을 고려할 수 있습니다.
3.1 선형성(Linearity)
- 종속 변수(예를 들면, 가격, 무게 등)와 독립 변수(예를 들면, 시간, 온도 등) 사이에는 직선과 같은 관계가 있어야 합니다. 즉, 한 변수가 변할 때 다른 변수도 예측 가능한 방식으로 변해야 합니다.
- 이 가정이 충족되지 않으면, 회귀 모델은 실제 데이터의 패턴을 잘못 해석할 수 있습니다.
3.2 오차의 독립성(Independence of Errors)
- 모델의 예측과 실제 값 사이의 차이(오차)가 서로 영향을 주지 않아야 합니다. 예를 들어, 오늘의 오차가 내일의 오차에 영향을 주면 안 됩니다.
- 오차가 서로 관련되어 있으면, 모델이 특정 패턴이나 추세를 놓칠 수 있습니다.
3.3 오차의 정규 분포(Normality of Errors)
- 오차는 '정규 분포'를 따라야 합니다. 즉, 오차가 특정한 '종모양'의 패턴을 보여야 합니다.
- 이 가정을 통해 통계적 추정과 검정이 더 정확하고 신뢰할 수 있게 됩니다.
3.4 오차의 등분산성(Homoscedasticity)
- 오차의 크기가 독립 변수의 값에 관계없이 일정해야 합니다. 즉, 독립 변수가 어떤 값이든 오차의 분산이 같아야 합니다.
- 이 가정이 위반되면, 모델이 데이터의 일부 영역에서는 잘 작동하지만 다른 영역에서는 잘 작동하지 않을 수 있습니다.
3.5 다중공선성(Multicollinearity) 부재
- 독립 변수들이 서로 너무 강하게 연관되어 있지 않아야 합니다. 즉, 하나의 독립 변수가 다른 독립 변수를 예측하는 데 사용되지 않아야 합니다.
- 다중공선성이 높으면, 어떤 독립 변수가 종속 변수에 영향을 미치는지 정확히 파악하기 어려워집니다.
4. 회귀 모형 평가
4.1 회귀 모형 적합도 평가
4.1.1 결정 계수(R-squared)
- R-제곱은 모델이 데이터의 변동성을 얼마나 잘 설명하는지를 나타내는 지표입니다.
- 값은 0과 1 사이에서 변하며, 1에 가까울수록 모델이 데이터를 더 잘 설명한다는 의미입니다.
- 하지만, 무조건 높은 R-제곱이 좋은 모델을 의미하지는 않으며, 과적합(overfitting)의 가능성도 고려해야 합니다.
4.1.2 조정된 결정 계수(Adjusted R-squared)
- 독립 변수의 수가 증가할 때 R-제곱의 증가를 보정합니다.
- 독립 변수의 수를 고려하여 R-제곱을 조정한 값으로, 불필요한 변수가 모델에 추가될 때 패널티를 부여합니다.
4.1.3 표준 오차(Standard Error)
- 회귀선과 실제 데이터 포인트 간의 평균 거리를 나타냅니다.
- 표준 오차가 작을수록 모델의 예측이 실제 값에 더 가깝다는 의미입니다.
4.1.4 F-통계량 (F-Statistic)
- 모델의 전체 유의성을 평가합니다.
- F-통계량이 크고, 관련 p-값이 작을수록 모델이 통계적으로 유의미하다고 간주됩니다.
4.1.5. AIC (Akaike Information Criterion) 및 BIC (Bayesian Information Criterion)
- 모델의 복잡성과 적합도를 함께 고려하는 지표입니다.
- 값이 작을수록 더 좋은 모델로 평가됩니다.
4.2. 회귀계수에 대한 T검정
이 검정의 주요 목적은 회귀 모델에서 각 독립 변수가 종속 변수에 미치는 영향이 통계적으로 유의미한지를 평가하는 것입니다. 구체적으로 다음과 같은 이유로 t 검정을 수행합니다
- 통계적 유의성 판단: t 검정은 각 독립 변수의 회귀계수가 0인지 아닌지를 판단합니다. 회귀계수가 0이라면, 해당 변수는 종속 변수에 영향을 미치지 않는 것으로 간주됩니다.
- 신뢰 구간 추정: t 검정은 회귀계수의 신뢰 구간(Confidence Interval)을 계산하는 데 사용됩니다. 신뢰 구간은 회귀계수가 특정한 범위 안에 있을 확률을 제공합니다.
- 변수 선택: 회귀 모델에서 어떤 변수들이 결과에 중요한 영향을 미치는지 결정하는 데 t 검정 결과가 사용될 수 있습니다. 통계적으로 유의미하지 않은 변수는 모델에서 제외할 수 있습니다.
- 모델의 예측력 평가: t 검정은 모델의 전체적인 예측력을 평가하는 데 도움을 줍니다. 모든 독립 변수의 계수가 유의미하다면, 모델은 데이터를 잘 설명할 가능성이 높습니다.
'머신러닝 > 머신러닝: 입문 개념' 카테고리의 다른 글
| 모델학습과 예측 (0) | 2024.12.01 |
|---|---|
| 분류(Classification) (3) | 2024.11.30 |
| 로지스틱 회귀분석 (0) | 2024.11.28 |
| 명목형(Nominal) 변수 인코딩 (2) | 2024.11.27 |
| 순서형(Ordinal) 변수 인코딩 (1) | 2024.11.26 |