1. 데이터 로드
import pandas as pd
import numpy as np
train_building = pd.read_csv("building_mart87_power_processed.csv")
train_building['date_time'] = pd.to_datetime(train_building['date_time'])
display(train_building.head())
display(f"{train_building['date_time'].min()}~ {train_building['date_time'].max()}")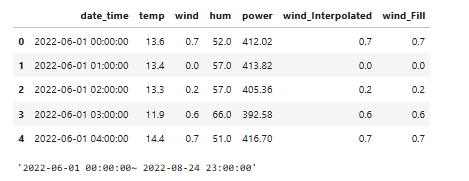
2. 시간별, 요일별 평균 전력 소비량 분석
import matplotlib.pyplot as plt
df = train_building.copy()
# 시간별 power의 평균 계산
hourly_power = df.groupby(df['date_time'].dt.hour)['power'].mean()
# 요일별 power의 평균 계산
weekly_power = df.groupby(df['date_time'].dt.weekday)['power'].mean()
display(hourly_power)
display(weekly_power)date_time
0 636.847412
1 586.117059
2 567.134471
3 523.389176
4 557.000471
5 655.912588
6 797.699647
7 1001.745529
8 1541.318824
9 1838.949882
10 1857.193412
11 1848.894353
12 1848.180706
13 1847.689412
14 1856.326235
15 1828.778824
16 1824.094588
17 1779.372000
18 1773.295412
19 1645.225412
20 1448.000471
21 1115.505529
22 844.788706
23 727.500706
Name: power, dtype: float64date_time
0 1336.897500
1 1323.391875
2 1299.189231
3 1293.974063
4 1314.925000
5 1352.656250
6 1105.532500
Name: power, dtype: float64
# 시각화
plt.figure(figsize=(10, 6))
# 시간별 power
plt.subplot(2, 1, 1)
hourly_power.plot(kind='bar', color='skyblue')
plt.title('Hourly Average Power Consumption')
plt.xlabel('Hour of Day')
plt.ylabel('Average Power')
# 요일별 power
plt.subplot(2, 1, 2)
weekly_power.plot(kind='bar', color='orange')
plt.title('Weekly Average Power Consumption')
plt.xlabel('Day of Week (0=Monday, 6=Sunday)')
plt.ylabel('Average Power')
plt.tight_layout()
plt.show()
※ 결과 해석
시각화를 통해 시간별 전력 소비 패턴을 살펴보면, 다음과 같은 특징을 발견할 수 있습니다.
- 새벽 시간대 (0시~6시): 전력 소비량이 상대적으로 낮습니다. 이 시간대는 대부분의 사람들이 자는 시간으로, 전력 사용이 적은 것이 당연할 수 있습니다.
- 오전 시간대 (7시~9시): 전력 소비량이 급격히 증가합니다. 이 시간대는 사람들이 일과를 시작하면서 전기 사용이 크게 증가하는 시기입니다.
- 오전 10시~오후 4시: 전력 소비량이 가장 높은 수준을 유지합니다. 이는 주로 업무 시간 동안 전력 소비가 집중되기 때문으로 보입니다.
- 저녁 시간대 (5시~9시): 전력 소비량이 서서히 감소하지만 여전히 높은 수준을 유지합니다. 이후 점차 전력 소비량이 감소하며 하루가 마무리됩니다.
이러한 시간대별 패턴을 바탕으로, 특정 시간대에 따른 파생 변수를 생성하는 것이 유용할 수 있습니다.
예를 들어, "아침", "오후", "저녁", "밤" 등으로 시간을 구분하는 변수를 만들어 전력 소비 패턴을 더 세밀하게 분석할 수 있습니다.
요일별 전력 소비 패턴을 분석해 보겠습니다.
- 일요일 (요일 6): 다른 요일에 비해 전력 소비량이 현저히 낮은 것을 볼 수 있습니다. 이는 주말 동안 활동이 감소하는 경향을 반영합니다.
- 평일 (월요일~토요일): 전력 소비량이 전반적으로 비슷한 수준을 유지하며, 큰 차이가 없습니다. 이는 평일 동안 일반적인 전력 소비 패턴이 유지되기 때문일 것입니다.
이 결과는 "주말(일요일)과 주중" 을 구분하는 파생 변수를 생성하는 데 중요한 근거를 제공합니다.
주중과 주말의 전력 소비 차이를 모델링하여 예측 성능을 높일 수 있습니다.
따라서, 시간대와 요일별로 전력 소비 패턴이 다르게 나타나기 때문에, 이를 반영한 파생 변수를 생성하는 것이 데이터를 더욱 효과적으로 분석하고 모델링하는 데 유용할 것으로 판단됩니다.
3. 시간대 및 주말/주중 구분 파생 변수 생성
# 시간 파생 변수 생성 (0=00시, 23=23시)
df['hour'] = df['date_time'].dt.hour
# 시간대 파생 변수 생성 (아침, 오후, 저녁, 밤)
def get_period_of_day(hour):
if 5 <= hour < 12:
return 'Morning'
elif 12 <= hour < 17:
return 'Afternoon'
elif 17 <= hour < 21:
return 'Evening'
else:
return 'Night'
df['period_of_day'] = df['hour'].apply(get_period_of_day)
# 주중/주말 구분 파생 변수 생성 (1=주말, 0=주중)
df['is_weekend'] = df['date_time'].dt.weekday.apply(lambda x: 1 if x >= 5 else 0)
# 결과 확인
df[['date_time', 'hour', 'period_of_day', 'is_weekend']].head(10)
4. 시간(hour), 월(month), 요일(day of week) 등의 순환적 특성 표현
※ 시간과 요일의 순환적 특성 반영
시간과 요일은 순환적 특성을 가지고 있습니다.
예를 들어, 시간이 23시에서 0시로 넘어가면서 하루가 다시 시작되고, 일요일이 지나면 다시 월요일이 오게 됩니다.
하지만, 이러한 순환적 특성을 단순히 정수로 표현할 경우, 모델은 23시와 0시, 일요일과 월요일의 연속적인 시간이라는 사실을 잘 인식하지 못할 수 있습니다.
이 문제를 해결하기 위해 사인(Sine)과 코사인(Cosine) 변수를 사용하여 시간과 요일을 표현하는 방법이 유용합니다.
이러한 방법은 주기성을 잘 반영할 수 있어, 모델이 시간과 요일의 특성을 더 잘 학습할 수 있습니다.
※ 시간(hour) 순환적 특성 표현
먼저, 하루 24시간을 기준으로 시간을 사인과 코사인 값으로 변환해 보겠습니다.
이를 통해 0시와 23시가 서로 연속된 시간이라는 것을 모델이 인식할 수 있습니다.
시간(hour) 순환적 특성 표현
train['hour_sin'] = np.sin(2 * np.pi * train['date_time'].dt.hour / 24)
train['hour_cos'] = np.cos(2 * np.pi * train['date_time'].dt.hour / 24)
이 코드에서는 date_time 컬럼에서 시간을 추출한 후, 이를 사인과 코사인 함수로 변환합니다.
23시와 0시가 서로 가깝게 이어진 순환적인 패턴을 나타내며, 시간대의 주기성을 효과적으로 반영합니다.
- hour_sin: 시계열 데이터를 0시에서 12시로 갈수록 증가하다가, 12시에서 24시로 갈수록 다시 감소하는 패턴을 표현합니다.
- hour_cos: 시계열 데이터를 0시에서 6시로 증가하다가, 6시에서 18시까지는 감소한 후, 18시에서 다시 증가하는 패턴을 표현합니다.
이러한 변환을 통해 모델이 시간의 순환성을 인식하도록 합니다.
※ 요일(day of week) 순환적 특성 표현
다음으로, 요일의 순환적 특성을 표현해 보겠습니다.
요일도 월요일부터 일요일까지 주기적으로 반복되므로, 이를 사인과 코사인 값으로 변환하여 주기성을 반영할 수 있습니다.
요일(day of week) 순환적 특성 표현
train['dayofweek_sin'] = np.sin(2 * np.pi * train['date_time'].dt.weekday / 7)
train['dayofweek_cos'] = np.cos(2 * np.pi * train['date_time'].dt.weekday / 7)
여기서 weekday는 월요일(0)부터 일요일(6)까지 숫자로 변환한 후, 이를 사인과 코사인 값으로 변환합니다.
이렇게 변환된 값은 요일 간의 연속성을 반영하여 주기적인 패턴을 더 잘 표현합니다.
- dayofweek_sin: 요일을 변환한 사인 값이 주중과 주말의 연속된 패턴으로 나타나며, 주기성을 반영합니다.
- dayofweek_cos: 주중과 주말을 더욱 명확하게 구분하며, 특정 요일의 주간적 패턴을 나타냅니다.
※ 어떤 데이터에서 이러한 순환적 특성 표현이 유용한가
이러한 특성 표현은 특히 주기적인 패턴이 중요한 데이터에서 유용합니다.
예를 들어, 에너지 소비량, 교통량, 웹사이트 방문자 수 등의 데이터는 시간대나 요일에 따라 주기적인 변동을 보일 수 있습니다.
이러한 데이터를 분석할 때, 사인과 코사인 변환을 통해 주기성을 반영한 파생 변수를 생성하면, 모델이 시간이나 요일의 특성을 더 잘 이해할 수 있습니다.
또한, 이러한 변환은 일반적으로 모델의 성능을 개선하는 데 도움을 줄 수 있습니다.
시간이나 요일에 따라 발생하는 패턴을 효과적으로 모델링할 수 있기 때문에, 예측 정확도를 높이는 데 기여할 수 있습니다.
시간과 요일의 순환적 특성을 표현할수 있고 특정 도메인 지식이나 데이터 탐색(EDA) 결과에 따라 월(month)이나 계절(season)과 같은 다른 시간 관련 요소들도 유사한 방식으로 변환할 수 있습니다.
이러한 변환은 도메인의 특성과 데이터를 깊이 이해하는 데 바탕을 두어야 하며, 교차 검증이나 Feature Selection 과정을 통해 최종적으로 모델에 포함할 파생 변수를 선택하는 것이 좋습니다.
import pandas as pd
# 시간(hour) 순환적 특성 표현
df['hour_sin'] = np.sin(2 * np.pi * df['date_time'].dt.hour/ 24)
df['hour_cos'] = np.cos(2 * np.pi * df['date_time'].dt.hour / 24)
# 요일(day of week) 순환적 특성 표현
df['dayofweek_sin'] = np.sin(2 * np.pi * df['date_time'].dt.weekday / 7)
df['dayofweek_cos'] = np.cos(2 * np.pi * df['date_time'].dt.weekday/ 7)
# 결과 확인
df[['date_time', 'hour_sin', 'hour_cos', 'dayofweek_sin', 'dayofweek_cos']].head()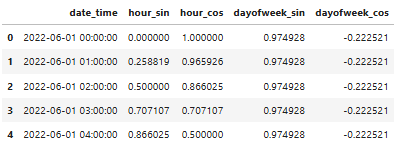
5. 시계열 데이터 정상성(Stationarity)
※ 시계열 데이터에서 정상성
시계열 분석에서 정상성(Stationarity)은 매우 중요한 개념입니다.
시계열 데이터가 정상성을 가지려면, 데이터의 통계적 특성(예: 평균, 분산, 자기상관)이 시간이 지나도 일정하게 유지되어야 합니다.
이는 시계열 모델링의 기초가 되는 중요한 가정 중 하나로, 많은 시계열 모델이 데이터가 정상성을 가진다고 가정하고 작동합니다.
정상성의 개념은 크게 두 가지로 나눌 수 있습니다: 강한 정상성(Strict Stationarity) 과 약한 정상성(Weak Stationarity) 입니다.
1) 강한 정상성(Strict Stationarity)
강한 정상성은 시계열 데이터의 분포가 시간에 따라 변하지 않는 경우를 의미합니다.
즉, 데이터의 평균, 분산뿐만 아니라 전체 분포가 시간에 따라 일정하게 유지됩니다.
강한 정상성을 만족하는 시계열 데이터는 모든 시점에서 동일한 확률 분포를 가집니다.
하지만, 이 조건은 매우 엄격하기 때문에 실제 데이터에서 강한 정상성을 확인하는 것은 어렵습니다.
2) 약한 정상성(Weak Stationarity)
약한 정상성은 시계열 데이터의 평균, 분산, 그리고 자기공분산이 시간에 따라 일정하게 유지되는 경우를 의미합니다.
이는 시계열 분석에서 더 자주 사용되는 개념입니다.
약한 정상성을 가진 데이터는 다음 세 가지 조건을 만족해야 합니다:
- 평균의 일정성: 데이터의 평균이 시간에 따라 변하지 않습니다.
- 분산의 일정성: 데이터의 분산도 시간에 따라 변하지 않습니다.
- 자기공분산의 시간 차이(시차) 의존: 데이터의 자기공분산이 시간의 절대적인 위치에 의존하지 않고, 시간 차이(lag)에만 의존합니다.
예를 들어, 오늘의 기온과 어제의 기온 차이가 일주일 후 기온과 12일 후 기온 차이와 비슷하다면, 이는 자기공분산이 시간 차이에만 의존한다고 볼 수 있습니다.
계절에 상관없이 하루 간격의 기온 변화 패턴이 비슷하다는 뜻입니다.
3) 비정상성(Non-Stationarity) 시계열 데이터
비정상성을 가지는 데이터는 시계열 모델링에서 문제를 일으킬 수 있습니다.
특히 ARIMA 모델 등 선형 모델은 데이터를 정상성 상태로 가정하고 분석을 수행하기 때문에, 비정상 데이터에 대해서는 제대로 작동하지 않을 수 있습니다.
예를 들어, 추세를 가지는 데이터나 계절성을 가지는 데이터는 일반적으로 비정상성을 가집니다.
계절성을 가진 데이터는 평균과 분산이 시간에 따라 변하거나, 계절적인 주기는 주기적인 변동을 보입니다.
※ 정상성과 비정상성 시계열 데이터의 예시
1) 정상성 시계열 데이터
아래 이미지는 정상성을 가진 시계열 데이터의 예시입니다.
이 데이터는 시간에 따라 일정한 평균과 분산을 유지하고 있습니다.

2) 비정상 시계열 데이터
아래 이미지는 시간이 지남에 따라 점차 증가하는 트렌드를 보이며, 평균이 시간이 지남에 따라 변하는 비정상 시계열 데이터의 예시입니다.

3) 비정상 시계열 데이터 (계절성)
이 데이터는 일정한 주기를 가지고 변동하며, 계절적 패턴이 뚜렷하게 나타납니다.
이러한 계절성은 데이터가 주기적으로 상승하거나 하락하는 패턴을 보여줍니다. 예를 들어, 데이터는 매월 초에 하락하고, 이후 중반에 상승하는 주기를 반복하고 있습니다.
이러한 특징은 시계열 데이터에서 특정 시점의 값이 이전 주기의 특정 시점과 유사한 경향을 보이는 것을 의미하며, 이는 데이터가 비정상성을 가지고 있다는 것을 시사합니다.

※ 정상성 여부 파악
정상성 여부를 파악하는 것은 시계열 데이터 분석에서 매우 중요한 단계입니다.
정상성을 가진 데이터는 시간이 지남에 따라 통계적 성질이 일정하게 유지되기 때문에, 이를 기반으로 한 모델은 데이터의 패턴을 더 정확하게 학습하고 예측할 수 있습니다.
정상성 분석은 대표적으로 다음과 같은 상황에서 필수적입니다:
- 예측 모델의 안정성: 정상성을 가지는 데이터는 예측 모델이 데이터의 일관된 패턴을 더 잘 학습할 수 있게 해줍니다. 이를 통해 예측의 신뢰성을 높일 수 있으며, 데이터의 변동에 따른 예측 오차를 줄이는 데 도움이 됩니다.
- ARIMA와 같은 시계열 모델: ARIMA(Autoregressive Integrated Moving Average) 모델과 같은 전통적인 시계열 모델은 데이터가 정상성을 가진다는 전제하에 작동합니다. 비정상성을 가진 데이터를 ARIMA 모델에 적용하면 부정확한 결과를 초래할 수 있기 때문에, 이러한 모델을 적용하기 전에 정상성 여부를 반드시 확인해야 합니다.
시계열 데이터가 정상성을 가지면, 데이터의 패턴을 더 쉽게 모델링하고 예측할 수 있습니다.
이를 확인하기 위해 ADF(Augmented Dickey-Fuller) 테스트와 같은 통계적 검정 기법이 사용됩니다.
ADF 테스트는 데이터가 정상성을 가지는지, 시간이 따라 평균과 분산이 일정한지를 평가하는 데 도움을 줍니다.
만약 데이터가 비정상성을 가진다면, 이를 정상성으로 변환하기 위해 차분(differencing), 로그 변환(log transformation) 등의 기법이 사용될 수 있습니다.
이러한 변환을 통해 데이터를 더욱 안정적으로 만들고, 모델링과 예측의 정확성을 높일 수 있습니다.
6. 정상성(Stationarity) 분석 및 ADF 테스트
정상성(Stationarity)은 시계열 분석에서 매우 중요한 개념입니다.
정상적인 시계열 데이터는 예측 모델을 구축할 때 더 안정적인 결과를 제공하며, 이를 바탕으로 하는 분석이 더 신뢰할 수 있습니다.
정상성이란 시계열 데이터의 통계적 성질(평균, 분산 등)이 시간에 따라 변하지 않는 상태를 의미합니다.
즉, 데이터가 시간에 따라 일정한 패턴을 유지하며, 이러한 특성이 변하지 않으면 정상성을 가진다고 할 수 있습니다.
1) 먼저 '시간'별로 기록된 'hourly'데이터를 '일별'('daily)데이터로 다운 샘플림을 수행하고, 이를 시각화 합니다.
import matplotlib.pyplot as plt
daily_data = train_building.copy()
daily_data = daily_data.set_index('date_time')
daily_data = daily_data.resample('D').mean()
# 시계열 데이터 시각화
plt.figure(figsize=(10, 6))
plt.plot(daily_data['power'], label='Power Consumption')
plt.title('Power Consumption Over Time')
plt.xlabel('Date')
plt.ylabel('Power Consumption')
plt.legend()
plt.show()
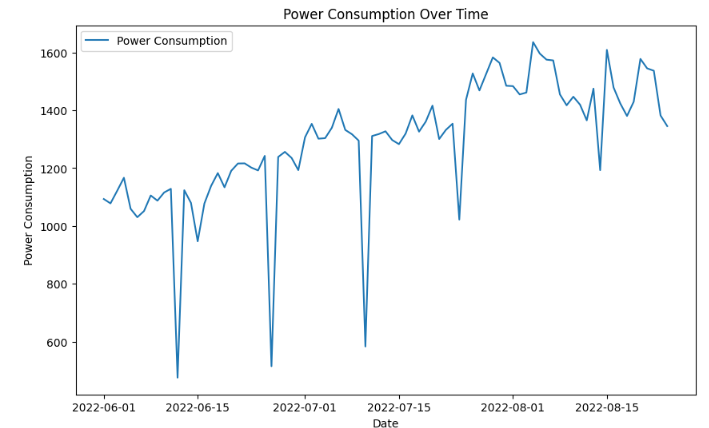
2) ADF 테스트를 통한 성상성 검증
※ ADF 테스트
정상성을 평가하기 위해 ADF(Augmented Dickey-Fuller) 테스트를 수행합니다.
ADF 테스트는 시계열 데이터가 정상성을 가지고 있는지, 즉 데이터가 일정한 평균과 분산을 유지하는지를 검증하는 데 사용되는 통계적 검정입니다. 이값이 더 작을수록 데이터가 정상성을 가질 가능성이 높습니다.
- ADF(augmented Dickey-Fuller) 테스트는 시계열 데이터의 안정성을 확인하기 위한 통계적 검정입니다. adfuller() 함수를 사용하여 ADF 테스트를 수행합니다.
- adfuller() 함수는 statsmodels.tsa.stattools 모듈에서 가져옵니다.
from statsmodels.tsa.stattools import adfuller
# ADF 테스트 함수
def adf_test(series):
result = adfuller(series)
print('ADF Statistic:', result[0])
print('p-value:', result[1])
print('Critical Values:')
for key, value in result[4].items():
print(f' {key}: {value}')
# ADF 테스트 실행
adf_test(daily_data['power'])ADF Statistic: -2.2817378051251858
p-value: 0.17792555308125596
Critical Values:
1%: -3.512738056978279
5%: -2.8974898650628984
10%: -2.585948732897085
※ 결과 해석
- ADF Statistic : 검정 통계량으로, 이 값이 음수로 더 작을수록(즉, 더 큰 음수일수록) 데이터가 정상성을 가질 가능성이 높습니다.
- p-value : 귀무가설(데이터가 비정상성을 가진다)을 기각할 수 있는지 판단하는 확률 값입니다. 일반적으로 p-value가 0.05보다 작으면 데이터가 정상성을 가진다고 결론 내릴 수 있습니다.
- Critical Values : 특정 신뢰 수준(1%, 5%, 10%)에서의 임계값을 나타냅니다. ADF 통계량이 이 임계값보다 작다면, 해당 신뢰 수준에서 귀무가설을 기각할 수 있습니다.
- Other outputs : 반환되는 튜플에는 이 외에도 데이터의 차수, 사용된 래그의 개수 등의 추가 정보가 포함되어 있습니다.
ADF 테스트 결과 해석
- ADF Statistic: -2.2817
- p-value: 0.1779
- Critical Values:
- 1%: -3.5127
- 5%: -2.8975
- 10%: -2.5859
ADF 테스트 결과를 해석하면, ADF 통계량이 -2.2817로 나타났고, p-value는 0.1779입니다.
p-value가 0.05보다 크기 때문에, 이 데이터는 비정상성을 가진다고 결론을 내릴 수 있습니다.
또한, Critical Values와 비교해도 ADF 통계량이 임계값보다 크기 때문에, 동일한 결론을 도출할 수 있습니다.
즉, 이 시계열 데이터는 정상성을 가지지 않으며, 시간이 따라 평균이 변하고 분산이 변화하고 있음을 의미합니다.
※ 정상성 확보의 필요성과 다음 단계
정상성을 확보하지 않은 비정상 시계열 데이터는 예측 모델이 시간에 따라 변화하는 패턴을 학습하는 데 어려움을 겪을 수 있습니다.
특히, ARIMA와 같은 전통적인 시계열 모델은 데이터가 정상성을 가진다고 가정해야 작동하기 때문에, 이러한 모델을 사용하기 전에 데이터를 정상성 상태로 변환하는 것이 필수적입니다.
정상성을 확보하면 모델이 데이터의 일관된 패턴을 학습할 수 있어 예측의 안정성과 정확성을 높일 수 있습니다.
하지만, 트리 기반 모델(LightGBM, XGBoost) 이나 딥러닝 모델(LSTM, GRU) 과 같은 경우에는 정상성을 반드시 요구하지 않습니다.
이들 모델은 비정상성을 가진 데이터에서도 효과적으로 작동할 수 있으며, 데이터 내에서 보다 복잡한 변동 패턴을 학습할 수 있습니다.
그럼에도 불구하고, 차분(differencing) 이나 로그 변환 같은 기법을 사용하여 장기적인 트렌드나 계절성을 제거하거나 완화하면, 모델이 단기적인 변동성이나 특정 주기적 패턴을 더 명확하게 학습할 수 있습니다.
이는 모델이 복잡한 비정상성 요소에 의해 혼란을 겪지 않고, 데이터의 중요한 패턴을 효과적으로 포착할 수 있도록 도와줍니다.
7. 차분(Differencing) 특성 생성
차분(Differencing)은 시계열 데이터의 정상성을 확보하기 위한 가장 일반적인 기법 중 하나입니다.
데이터의 연속된 시점 간의 차이를 계산함으로써, 데이터에 포함된 트렌드나 계절성과 같은 장기적인 패턴을 제거하거나 완화하여 데이터가 정상성을 가지도록 합니다.
이는 특히 ARIMA 모델과 같은 정상성을 전제로 한 시계열 모델에서 중요한 전처리 과정입니다.
- 시계열 데이터의 추세나 계절성을 제거하기 위해 차분(differencing)을 수행합니다. 이를 위해 diff() 메서드를 사용합니다.
- diff() 메서드는 데이터의 차분을 계산하여 이전 값과의 차이를 구합니다. 차분 계산 후에는 dropna() 메서드를 사용하여 NaN 값을 제거합니다.
# 1차 차분(differencing) 적용
daily_data_diff = daily_data['power'].diff().dropna()
# 차분된 데이터 시각화
plt.figure(figsize=(10, 6))
plt.plot(daily_data_diff, label='Differenced Power Consumption')
plt.title('Differenced Power Consumption Over Time')
plt.xlabel('Date')
plt.ylabel('Differenced Power Consumption')
plt.legend()
plt.show()
- 차분 후의 데이터를 ADF 테스트로 정상성을 검증합니다.
# ADF 테스트 함수
def adf_test(series):
result = adfuller(series)
print('ADF Statistic:', result[0])
print('p-value:', result[1])
print('Critical Values:')
for key, value in result[4].items():
print(f' {key}: {value}')
# 차분 후 ADF 테스트 실행
adf_test(daily_data_diff)ADF Statistic: -7.140385192821452
p-value: 3.3360454655429817e-10
Critical Values:
1%: -3.526004646825607
5%: -2.9032002348069774
10%: -2.5889948363419957
※ 결과 해석
차분을 적용한 후의 그래프에서는 데이터의 변동성이 이전보다 일정해졌으며, 장기적인 트렌드가 제거된 것을 확인할 수 있습니다. 이러한 변환을 통해 데이터가 정상성 상태에 더 가까워졌다고 판단할 수 있습니다.
차분된 데이터에 대해 다시 ADF 테스트를 수행한 결과는 다음과 같습니다:
- ADF Statistic: -7.1404
- p-value: 3.336e-10
- Critical Values:
- 1%: -3.5260
- 5%: -2.9032
- 10%: -2.5890
ADF 통계량이 -7.1404로 나타났고, p-value가 0.05보다 훨씬 작은 값(3.336e-10)을 가집니다.
이는 데이터가 정상성을 확보했다는 증거입니다.
Critical Values와 비교해도 ADF 통계량이 모든 임계값보다 작기 때문에, 차분을 통해 비정상성이 제거되고 데이터가 정상성을 갖게 되었음을 확인할 수 있습니다.
8. ACF(자동상관 함수)와 PACF(부분자동상관 함수) 개요
시계열 데이터에서 과거의 값이 현재의 값에 어떻게 영향을 미치는지를 이해하는 것은 매우 중요합니다.
이때 유용하게 사용되는 도구가 ACF(Autocorrelation Function) 와 PACF(Partial Autocorrelation Function) 입니다.
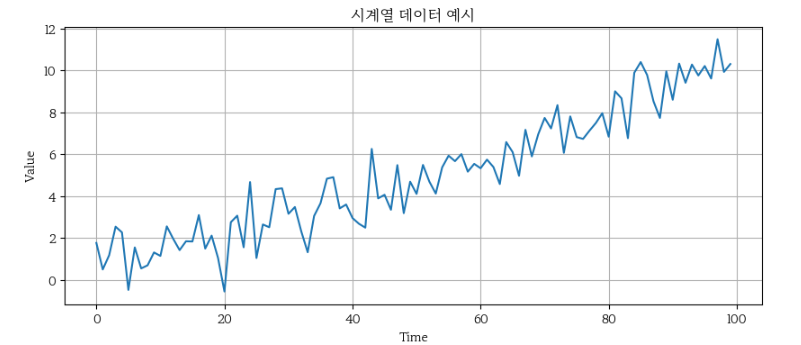
위의 시계열 데이터는 시간이 지남에 따라 점차 증가하는 패턴을 보여주고 있습니다.
데이터의 초기 값들은 상대적으로 낮은 수준에서 변동을 보이지만, 시간이 지남에 따라 데이터의 값은 전반적으로 상승하는 경향을 보입니다.
이 그래프는 데이터에 트렌드가 존재함을 시사하며, 이는 비정상성의 대표적인 예 중 하나입니다.
이러한 트렌드를 분석하고 제거하기 위해 ACF와 PACF 분석을 활용할 수 있습니다.
※ ACF(자동상관 함수)
ACF는 시계열 데이터의 특정 시점과 그 이전의 여러 시점(lag) 간의 상관관계를 측정하는 함수입니다.
예를 들어, 오늘의 값이 어제의 값이나 일주일 전의 값과 관련이 있는지를 측정합니다.
ACF는 이러한 상관관계를 계산하여 그래프로 시각화할 수 있습니다.

ACF(자동상관 함수) 그래프에서 x축은 lag을 나타내며, y축은 해당 lag에서의 상관관계 계수를 나타냅니다.
위의 그래프에서는 lag 1에서 높은 상관관계가 나타나고, lag이 커질수록 상관관계가 점차 감소하는 것을 볼 수 있습니다. 이는 시간 차이가 커질수록 과거의 데이터가 현재 데이터에 미치는 영향이 줄어든다는 것을 의미합니다.
이러한 ACF 패턴은 비정상성을 나타낼 수 있습니다.
예를 들어, lag 값이 느리게 감소하는 경향이 있다면, 데이터에 트렌드(추세) 나 계절성이 존재할 가능성이 큽니다.
정상적인 시계열 데이터는 일반적으로 ACF 값이 빠르게 0에 수렴하는 경향을 보입니다.
하지만 위의 그래프처럼 점진적으로 감소하는 ACF 패턴은 시계열 데이터가 시간에 따른 트렌드 또는 계절적 변동을 가지고 있을 수 있다는 것을 시사합니다.
※ PACF(부분자동상관 함수)
PACF는 특정 lag에서 그 이전 시점들의 영향을 제거한 후, 현재 시점과 그 lag 간의 상관관계를 측정합니다.
이는 중간에 있는 다른 시점들의 영향을 배제하고, 순수한 상관관계를 파악할 수 있게 해줍니다.
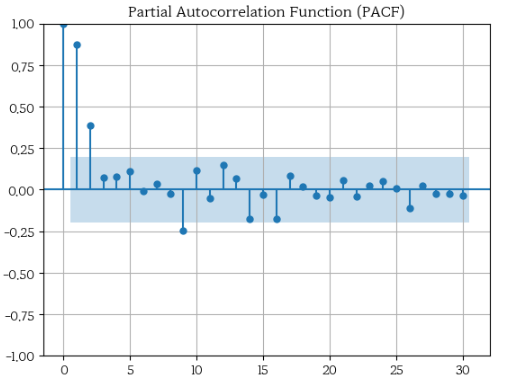
PACF 그래프에서 초기 lag (특히 lag 1, 2 등)에서는 큰 상관관계를 보이지만, 이후 lag에서는 급격히 감소합니다.
이는 데이터가 자기회귀적인 성향이 강하고, 특히 가까운 과거의 데이터가 현재 데이터에 큰 영향을 미친다는 것을 의미합니다. 이러한 패턴은 데이터에 트렌드가 있거나, 비정상적인 요소가 존재할 수 있음을 나타냅니다.
PACF에서 계절성은 특정 lag(예: lag 90)에서 주기적인 패턴에 관련되는 경우의 값을 통해 정량적으로 확인할 수 있습니다.
계절성은 데이터가 일정한 주기로 반복되는 패턴을 보이는 경우, 그 주기에 해당하는 lag에서 PACF 값이 높게 나타나는 특징을 가집니다.
예를 들어, 주간 패턴이 있는 경우 lag 9에서 PACF 값이 높게 나타날 수 있습니다.
반면에, 추세(트렌드)는 PACF에서 직접적으로 관찰하기 어렵습니다.
추세는 데이터가 장기적으로 일정한 방향으로 변화하는 경향을 말하며, 이는 PACF 값이 여러 lag에 걸쳐 서서히 감소하는 패턴으로 나타날 수 있습니다.
그러나, 추세를 정확히 정량화하려면 ADF 테스트와 같은 방법이 더 적합합니다.
추세가 있는 데이터는 보통 비정상성을 가지며, 이 경우 ACF/PACF 분석 이전에 추세를 제거하거나 차분을 통해 정상성을 확보하는 것이 필요합니다.
ACF와 PACF 분석은 시계열 모델링에서 특히 ARIMA(Autoregressive Integrated Moving Average) 모델의 주요 파라미터를 설정하는 데 사용됩니다.
ARIMA 모델의 (p차 자기회귀 차수), d(차분 횟수), q(이동평균 차수) 값을 결정하는 데 이 함수들이 유용합니다.
ACF와 PACF의 패턴을 통해 p와 q 값을 추정할 수 있으며, 데이터의 정상성 여부를 판단하여 d 값을 결정할 수 있습니다.
※ 파생 변수 생성
ACF와 PACF 분석을 통해 발견된 상관관계나 주기성을 바탕으로, 유용한 파생 변수를 생성할 수 있습니다.
- Lag 특성 변수 생성: PACF 그래프에서 특정 lag(예: lag 7)에 높은 상관관계가 나타난다면, 해당 lag에 해당하는 데이터를 새로운 특성으로 추가할 수 있습니다. 이는 주간 패턴이 존재하는 데이터에서 특히 유용합니다.
- 주기성 반영: ACF 그래프에서 특정 주기적인 패턴이 나타나는 경우, 해당 주기를 반영한 파생 변수를 생성할 수 있습니다. 예를 들어, 계절성을 가진 데이터에서 12개월 또는 7일 간격의 패턴이 뚜렷하다면, 이를 반영한 파생 변수를 추가해 모델의 예측 성능을 높일 수 있습니다.
9. ACF(자동상관 함수)와 PACF(부분자동상관 함수) 분석
ACF(자동상관 함수)와 PACF(부분자동상관 함수)는 시계열 데이터에서 시간 지연(lag)과 그에 따른 상관관계를 분석하는 데 중요한 도구입니다.
특히, ARIMA 모델링에서는 이 두 함수를 통해 p(AR), d(Difference), q(MA) 값을 결정하는 데 사용됩니다.
또한, 이 분석을 통해 시계열 예측 문제에서 의미 있는 파생 변수 생성의 아이디어를 얻을 수 있습니다.
※ ACF(Autocorrelation Function)
- 정의: ACF는 시계열 데이터의 특정 시점과 여러 지연된 시점(lag) 간의 상관관계를 측정하는 함수입니다. 이를 통해 과거 데이터가 현재 데이터에 어떻게 영향을 미치는지 파악할 수 있습니다.
- 활용: ACF는 주로 MA(Moving Average) 모델의 q 값을 결정하는 데 사용됩니다. ACF의 lag k에서 값이 급격히 감소하거나 일정한 패턴을 보일 때, q 값을 선택할 수 있습니다.
※ PACF(Partial Autocorrelation Function)
- 정의: PACF는 특정 lag에서 그 이전 시점들의 영향을 제거한 후, 현재 시점과 그 lag 간의 상관관계를 측정합니다.
- 활용: PACF는 주로 AR(Autoregressive) 모델의 p 값을 결정하는 데 사용됩니다. PACF의 lag k에서 값이 급격히 감소하거나 일정한 패턴을 보일 때, p 값을 선택할 수 있습니다.
이 두 가지 분석을 통해 시계열 데이터에서 특정 시점의 데이터가 현재 데이터에 어떻게 영향을 미치는지 파악할 수 있으며, 이를 바탕으로 효과적인 모델을 구축할 수 있습니다.
이제 자전거 수요 데이터를 활용하여 ACF(자동상관 함수) 와 PACF(부분자동상관 함수) 를 계산하고, 이를 시각화하여 분석해보겠습니다.
import matplotlib.pyplot as plt
bike_daily_demand = pd.read_csv("bike_demand_daily.csv")
bike_daily_demand['date_time'] = pd.to_datetime(bike_daily_demand['date_time'])
display(bike_daily_demand.head())
display(f"{bike_daily_demand['date_time'].min()}~ {bike_daily_demand['date_time'].max()}")
# 수요 데이터 시각화
plt.figure(figsize=(10, 4))
plt.plot(bike_daily_demand['date_time'], bike_daily_demand['demand'], label='Bike Demand')
plt.title('자전거 수요량')
plt.xlabel('Date')
plt.ylabel('수요량')
plt.legend()
plt.show()
- ACF(자동상관 함수)와 PACF(부분자동상관 함수)를 계산하고 시각화하기 위해 acf()와 pacf() 함수를 사용합니다. 이 함수들은 statsmodels.tsa.stattools 모듈에서 가져옵니다.
- ACF와 PACF를 시각화하기 위해 plot_acf()와 plot_pacf() 함수를 사용합니다. 이 함수들은 statsmodels.graphics.tsaplots 모듈에서 가져옵니다.
- nlags 매개변수는 계산할 시차(lag)의 수를 지정하며, alpha는 신뢰 구간을 계산하기 위한 유의 수준을 설정합니다.
from statsmodels.tsa.stattools import acf, pacf
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
# ACF(자동상관 함수) 계산 및 시각화
plt.figure(figsize=(10, 3))
plot_acf(bike_daily_demand.index, lags=50, alpha=0.05)
plt.title('Autocorrelation Function (ACF)')
plt.show()
# PACF(부분자동상관 함수) 계산 및 시각화
plt.figure(figsize=(10, 3))
plot_pacf(bike_daily_demand['demand'], lags=50, alpha=0.05)
plt.title('Partial Autocorrelation Function (PACF)')
plt.show()
# ACF와 PACF 값 계산
acf_values = acf(bike_daily_demand['demand'], nlags=50, alpha=0.05)
pacf_values = pacf(bike_daily_demand['demand'], nlags=50, alpha=0.05)
# ACF 값 출력 (각 lag에 대한 값)
print("ACF Values:")
print(acf_values[0])
# PACF 값 출력 (각 lag에 대한 값)
print("\nPACF Values:")
print(pacf_values[0])

※ Statsmodels의 acf, pacf, plot_acf, plot_pacf
1) acf (Autocorrelation Function)
acf 함수는 시계열 데이터의 자동상관(Autocorrelation) 을 계산하는 데 사용됩니다. 자동상관이란, 시계열 데이터가 시간의 흐름에 따라 얼마나 자기 자신과 상관관계를 가지는지를 나타내는 지표입니다. acf는 다양한 시간 차이(lag)에서의 상관관계를 계산하여 반환합니다.
acf_values = acf(bike_daily_demand['demand'], nlags=50, alpha=0.05)
위 코드는 bike_daily_demand['demand'] 데이터를 입력으로 받아, 최대 50개의 Lag에 대한 자동상관 계수를 계산합니다. alpha=0.05는 95% 신뢰 구간을 설정해줍니다. 함수는 ACF 값을 배열 형태로 반환합니다.
2) pacf (Partial Autocorrelation Function)
pacf 함수는 부분자동상관(Partial Autocorrelation) 을 계산합니다. 부분자동상관은 특정 Lag의 시점과 그 이전의 시점 간의 직접적인 상관관계를 측정합니다. 이는 중간에 있는 다른 시간값들의 영향을 배제한 순수한 상관관계입니다. pacf는 특히 AR(자기회귀) 모델에서 p(차수)를 결정하는 데 유용합니다.
pacf_values = pacf(bike_daily_demand['demand'], nlags=50, alpha=0.05)
pacf 함수는 acf와 유사하게 동작하지만, 각 Lag에서의 부분자동상관 계수를 반환합니다. 이 값은 시계열 데이터의 자기회귀 모형을 설정할 때 중요하게 사용됩니다.
3) plot_acf
plot_acf 함수는 시계열 데이터의 자동상관 함수를 시각화하는 데 사용됩니다. 이 함수는 다양한 Lag에 따른 자동상관 계수를 그래프 형태로 표현해주어, 시계열 데이터가 시간에 따라 어떻게 상관되는지 직관적으로 파악할 수 있게 해줍니다.
plot_acf(bike_daily_demand.index, lags=50, alpha=0.05)
이 코드는 bike_daily_demand 데이터의 ACF를 시각화합니다. 여기서 lags=50은 최대 50개의 Lag까지 시각화한다는 의미이며, alpha=0.05는 95% 신뢰 구간을 표시하기 위한 설정입니다. 결과는 ACF 그래프로 나타납니다.
4) plot_pacf
plot_pacf 함수는 부분자동상관 함수(PACF)를 시각화하는 함수로, 특정 Lag에 대한 순수한 상관관계를 시각적으로 표현해줍니다. 이 그래프를 통해 특정 Lag에서의 직접적인 상관관계가 얼마나 강한지 쉽게 이해할 수 있습니다.
plot_pacf(bike_daily_demand['demand'], lags=50, alpha=0.05)
이 코드는 bike_daily_demand 데이터의 PACF를 시각화합니다. 이 그래프는 각 Lag에서의 부분자동상관 계수를 보여주며, AR 모델에서 p(차수)를 결정하는 데 유용합니다. lags=50은 최대 50개의 Lag까지 시각화합니다.
※ 결과 해석
ACF 분석 결과
- lag 1에서 ACF 값이 매우 높게 나타났으며, 이는 바로 직전의 수요 데이터가 현재의 수요 데이터와 강한 상관관계를 가진다는 것을 의미합니다.
- lag가 증가함에 따라 ACF 값은 점차 감소하는 패턴을 보였으며, 이는 시간이 지남에 따라 과거 데이터의 영향이 점차 줄어든다는 것을 의미합니다.
PACF 분석 결과
- lag 1에서 PACF 값이 가장 높게 나타났으며, 이는 직전 시점의 데이터가 현재 시점의 수요에 가장 큰 독립적인 영향을 미친다는 것을 의미합니다.
- 특히, lag 7에서도 일정한 주기적인 패턴이 관찰되었습니다. 이는 주 단위의 주기성을 나타낼 수 있으며, 이 정보를 활용해 lag 7 특성을 생성할 수 있습니다.
- 이후 lag에 대한 PACF 값은 급격히 감소하였으며, 대부분의 lag는 통계적으로 유의미한 상관관계를 보이지 않았습니다.
※ 파생 변수 생성 아이디어
ACF와 PACF 분석을 통해 다음과 같은 파생 변수를 생성할 수 있습니다:
- Lag 1 특성 생성: PACF 분석 결과, lag 1이 현재 수요 데이터에 가장 큰 영향을 미친다는 것이 확인되었습니다. 따라서, lag 1의 데이터를 새로운 특성으로 추가함으로써 모델의 예측 성능을 향상시킬 수 있습니다.
- Lag 7 특성 생성: 주기적 패턴을 반영하기 위해, lag 7(1주일 전)의 데이터를 새로운 특성으로 추가할 수 있습니다. 이는 데이터의 주기성을 모델이 잘 반영할 수 있게 합니다.
이러한 파생 변수들은 예측 모델이 시계열 데이터의 패턴을 보다 잘 이해하고 반영할 수 있게 하며, 모델의 예측 성능을 높이는 데 기여할 수 있습니다.
하지만, 특성을 생성하기보다는 교차 검증 등의 과정을 통해 모델의 실제 성능에 미치는 영향을 면밀히 평가해야 합니다.
특정 특성이 모든 경우에 유용한 것은 아니므로, 데이터에 맞는 최적의 특성을 선택하는 과정이 중요합니다.
10. 지연(Lag) 특성 생성
Lag 특성은 과거의 데이터를 현재 시점의 예측 변수로 사용하는 방법으로, 데이터에 내재된 시간 의존성을 모델링에 반영할 수 있게 해줍니다.
특히, PACF 분석을 통해 특정 Lag에서 부분자동상관이 유의미하게 나타나는 경우, 해당 Lag 값을 특성으로 추가함으로써 모델의 예측 성능을 향상시킬 수 있습니다.
※ Lag 특성의 필요성
시계열 데이터는 시간의 흐름에 따라 연속된 값을 가지기 때문에, 현재의 데이터가 이전 시점의 데이터와 상관관계를 가질 가능성이 큽니다.
이러한 상관관계를 활용해 Lag 특성을 생성하면, 모델이 과거의 정보를 기반으로 미래를 예측하는 데 더 유리해집니다.
※ 특정 Lag 값 선택
PACF 분석 결과에서 lag-1, lag-2, lag-7에서 부분자동상관 계수가 유의미하게 나타났습니다.
이는 이전 날(lag=1), 이틀 전(lag=2), 그리고 일주일 전(lag=7) 의 수요 데이터가 현재의 수요를 예측하는 데 의미 있는 역할을 할 수 있음을 시사합니다.
bike_daily_demand['lag_1'] = bike_daily_demand['demand'].shift(1)
위 코드는 shift(1) 함수를 사용해 데이터를 1칸 아래로 이동시킵니다.
따라서, lag_1 특성은 이전 날의 수요 데이터를 현재 시점의 특성으로 가지게 됩니다.
※ 파생 특성 생성 후 처리
Lag 특성을 생성하면, 초기 몇 개의 행은 NaN 값으로 채워지게 됩니다.
이는 해당 시점에서 과거 데이터를 참조할 수 없기 때문에 발생하는 현상입니다.
이러한 NaN 값들은 모델 학습 전 적절히 제거하거나 처리해주는 것이 중요합니다.
모델에 새로운 특성을 추가할 때는 항상 검증을 거쳐 모델의 성능을 실제로 향상시키는지 평가해야 합니다.
불필요한 특성 추가는 오히려 모델의 성능을 저하시키는 경우도 있기 때문입니다.
- shift() 메서드를 사용하여 시계열 데이터의 Lag 특성을 생성할 수 있습니다. 이 메서드는 데이터를 지정된 만큼의 시차(lag)만큼 이동시킵니다.
- shift(1)은 데이터를 1 시차 만큼 이동시켜 lag_1 특성을 생성하며, shift(7)은 7 시차 만큼 이동시켜 lag_7 특성을 생성합니다.
# Lag 특성 생성
bike_daily_demand['lag_1'] = bike_daily_demand['demand'].shift(1)
bike_daily_demand['lag_7'] = bike_daily_demand['demand'].shift(7)
# 결과 확인
display(bike_daily_demand.head(10))

'딥러닝 > 딥러닝: 시계열 데이터' 카테고리의 다른 글
| RNN 구현 (0) | 2025.01.22 |
|---|---|
| RNN 원리와 구조 (0) | 2025.01.22 |
| 시계열 데이터 분석 및 전처리 (0) | 2025.01.21 |
| pandas를 활용한 날짜 및 시간 데이터 처리 (0) | 2025.01.21 |
| 시계열 데이터와 Python datetime (0) | 2025.01.20 |