1. 경사하강법(Gradient Descent)
1) 경사하강법
경사하강법은 손실 함수가 가장 낮은 값을 갖는 매개변수를 찾기 위한 방법입니다.
손실 함수의 기울기(미분)를 사용하며, 손실을 최소화하는 방향으로 매개변수를 조금씩 조정해 나갑니다.
기울기가 양의 방향이면 매개변수를 감소시키고, 기울기가 음의 방향이면 매개변수를 증가시켜 손실을 줄여나가는 과정을 반복합니다.
2) 왜 사용하는가?
모든 기계 학습 모델의 목표는 주어진 문제에 대해 최적의 예측을 하는 것입니다.
경사하강법은 이 목표를 달성하기 위해 모델의 손실을 최소화하기 위한 효율적이고 직관적인 방법을 제공합니다.
모델이 손실 값을 줄이도록 매개변수를 점진적으로 조정함으로써, 최적의 매개변수 값을 찾아내고, 더 높은 예측 정확도를 달성할 수 있도록 돕습니다.
3) 경사하강법의 문제점
※ 지역 최소값(Local Minimum)
손실 함수에 작은 '골짜기'가 여러 곳에 있을 때, 경사하강법이 이 중 하나에 멈추게 될 수 있습니다.
마치 산을 오른다고 할 때, 정상에 도달하기 전에 작은 언덕에서 멈추는 것과 같은 경우입니다.
우리가 원하는 것은 이 작은 능선이 아니라, 실제로 가장 낮은 곳, 즉 전역 최소값(Global Minimum)에 도달하는 것입니다.

이미지에는 두 개의 최소값이 있습니다.
하나는 전역 최소값(global minimum)으로, 가장 낮은 점을 나타내며 빨간색으로 표시되어 있습니다.
다른 하나는 지역(local minimum) 최소값으로, 더 높은 위치에 있으며 초록색으로 표시되어 있습니다.
경사 하강법을 시작하며, 우리는 마치 일정적으로 가속패달을 밟으며 "출발!"을 외치는 것처럼, 기울기의 방향을 따라 전진합니다.
"기울기가 양수네? 가중치를 감소시켜야겠어!"라는 말처럼, 우리는 기울기가 양의 방향일 때는 가중치를 줄여 손실 함수의 값을 낮추어야 한다는 것을 알고 있습니다.
이 과정에서 우리는 각 단계마다 낮은 손실 함수 값을 향해 나아갑니다.
이는 각 초록색 원으로 표현되며, 이것은 우리가 낮은 곳으로 잘 내려가고 있음을 나타냅니다.
하지만 어느 순간, "아싸 목표 달성했다!"라며 우리는 지역 최소값에 이르러 경사 하강법이 멈추어버립니다.
그때 누군가 지적합니다, "엥? 거긴 목표지점이 아니야! 거기보다 더 낮은 곳을 찾아봐."
우리는 전역 최소값, 즉 그래프에서 가장 낮은 점을 찾고자 하지만, 지역 최소값에서 기울기가 0이 되어버리면, "뭐? 조그만한 기울기가 0 이여서 이미 학습이 끝났어... 더 이상 이동할 수 없어"라는 판단에 도달하게 됩니다.
이는 모델의 최적화 성능을 발휘하기 위해서는 전역 최소값을 찾아야 하지만, 지역 최소값에 만족하며 추가적인 학습 없이 현재 상태에 머물 수 있음을 상기시켜 줍니다.
4) 경사하강법의 주요 특징
- 반복적 접근과 수렴성:
경사하강법은 반복적으로 기울기를 계산하고 매개변수를 업데이트합니다. 이 과정에서 알고리즘의 수렴성은 중요한 요소로, 적절한 조건 하에서 알고리즘은 로컬 미니멈 또는 글로벌 미니멈으로 수렴하게 됩니다. - 학습률(Learning Rate):
학습률은 이동의 크기를 결정합니다. 즉, 한 번에 얼마나 멀리 갈지를 결정하는 것입니다. 학습률이 너무 크면 최소값을 지나치게 되고, 너무 작으면 학습 속도가 매우 느려집니다. 적절한 학습률을 설정하는 것은 학습 과정의 효율성을 결정하는 중요한 요소입니다. - 글로벌 미니멈 추구:
가능한 한 손실 함수의 전역 최소값에 도달하려고 합니다. 그러나 실제로는 지역 최소값에 도달하는 경우도 많습니다.
5) 주의사항
- 학습률이 너무 크면 최소값을 지나쳐 발산할 수 있고, 너무 작으면 학습이 너무 느려져 최적점에 도달하기 전에 학습이 멈출 수 있습니다.
- 모든 문제에 대해 글로벌 미니멈을 보장하지는 않으며, 때로는 지역 미니멈에 갇힐 수 있습니다.
6) 경사하강법의 종류
경사하강법에는 주로 세 가지 변형이 있습니다: 배치 경사하강법, 미니 배치 경사하강법, 그리고 확률적 경사하강법. 이들 각각은 계산 효율성, 수렴 속도, 그리고 메모리 사용량의 측면에서 서로 다른 이점을 제공합니다.
※ 배치 경사하강법 (Batch Gradient Descent)
배치 경사하강법은 매 반복에서 전체 데이터 세트를 사용하여 그래디언트를 계산합니다.
- 이 방법은 정확한 그래디언트 방향을 제공하지만, 매우 큰 데이터 세트에 대해서는 계산 비용이 매우 높을 수 있습니다.
※ 미니 배치 경사하강법 (Mini-batch Gradient Descent)
미니 배치 경사하강법은 전체 데이터 세트를 작은 배치로 나누고, 각 반복에서 하나의 배치를 사용하여 그래디언트를 계산합니다.
- 이 방법은 계산 효율성과 수렴 속도 사이에 좋은 균형을 제공합니다.
※ 확률적 경사하강법 (Stochastic Gradient Descent, SGD)
확률적 경사하강법은 매 반복에서 단 하나의 샘플을 무작위로 선택하여 그래디언트를 계산합니다.
- 이 방법은 빠른 수렴 속도를 제공하지만, 경로가 불안정할 수 있으며, 최소값에 도달하더라도 계속해서 약간씩 변동할 수 있습니다.
※ 선택 기준
- 데이터 세트의 크기와 자원의 제약:
- 큰 데이터 세트의 경우, 미니 배치 경사하강법이 일반적으로 가장 좋은 성능을 제공합니다.
- 온라인 학습이나 매우 빠른 반복이 필요한 경우, 확률적 경사하강법을 고려할 수 있습니다.
각 방법의 선택은 특정 문제의 요구사항, 데이터의 크기, 그리고 계산 자원의 가용성에 따라 달라집니다. 이러한 경사하강법의 변형들을 이해하고 올바르게 선택하는 것은 모델의 학습 효율성과 성능을 최적화하는 데 중요합니다.
2. 확률적 경사하강법 (Stochastic Gradient Descent, SGD)
1) 확률적 경사하강법
확률적 경사하강법(SGD)은 경사하강법의 변형으로, 매 업데이트에서 전체 데이터셋 대신 무작위로 선택한 하나의 데이터 샘플을 사용하여 가중치를 조정합니다. 이 방법은 매우 큰 데이터셋에서 경사하강법을 더 효율적으로 적용할 수 있게 해주며, 각 단계에서 계산 비용을 크게 줄여줍니다.
2) 언제 왜 사용하는가
확률적 경사하강법은 특히 대규모 데이터셋에서 효율적입니다. 전체 데이터를 사용해 가중치를 업데이트하는 것은 계산 비용이 매우 높지만, SGD를 사용하면 이 비용을 상당히 줄일 수 있습니다. 또한, SGD는 지역 최소값에 갇혀버릴 수 있는 잠재력을 가지고 있어, 때로는 경사하강법보다 더 좋은 성능을 보일 수 있습니다.
3) 확률적 경사하강법의 장단점
장점
- 대규모 데이터셋에서 효율적이며 빠른 수렴 속도를 제공합니다.
- 지역 최소값에서 벗어날 가능성이 높아 글로벌 최솟값을 찾을 확률이 증가합니다.
단점
- 업데이트 과정에서 높은 변동성을 보여, 수렴 과정이 경사하강법에 비해 불안정할 수 있습니다.
- 최적화 과정에서 노이즈가 많아 학습 조정이 더 세심하게 이루어져야 합니다.
4) 해결 방안
- 변동성을 줄이기 위해 미니배치 경사하강법을 사용할 수 있습니다. 이는 한 번에 작은 데이터셋(미니배치)을 사용해 업데이트하는 방식으로, SGD의 효율성과 전체 배치 경사하강법의 안정성 사이의 균형을 제공합니다.
- 학습률 스케줄링 기법을 적용하여 학습 과정에서 학습률을 점진적으로 감소시키면 수렴을 촉진하고 결과적으로 더 안정적인 최적화를 달성할 수 있습니다.
5) 주의사항
- 적절한 학습률과 미니배치 크기의 선택이 중요합니다. 너무 크면 학습률이 발산으로 이어질 수 있고, 너무 작으면 학습이 느려질 수 있습니다.
6) 코드
- 첫 번째 빈칸에서는 옵티마이저로 optim.SGD를 사용해야 합니다. SGD는 모델의 파라미터에 대한 손실 함수의 기울기를 사용하여 파라미터를 업데이트하는 기본적인 최적화 알고리즘입니다.
- 옵티마이저를 초기화할 때 첫 번째 인자로는 모델의 파라미터를 제공해야 합니다. model.parameters()는 모델의 모든 학습 가능한 파라미터를 반환합니다.
- 두 번째 인자로는 학습률 lr을 설정해야 합니다. 학습률은 각 반복에서 파라미터를 얼마나 업데이트할지 결정하는 값으로, 여기서는 0.01로 설정됩니다.
import torch
import torch.nn as nn
import torch.optim as optim
model = nn.Linear(1, 1)
optimizer = optim.SGD(model.parameters(), lr=0.01)3. 학습률
1) 학습률
학습률은 기계 학습과 신경망에서 경사하강법을 사용할 때, 매개변수(또는 가중치)의 업데이트 크기를 결정하는 중요한 하이퍼파라미터입니다.
이는 모델이 학습하는 속도를 결정하며, 각 반복에서 매개변수를 얼마나 조정할지를 정의합니다.
우리는 신경망을 반복적으로 훈련시켜서 우리의 목표 지점을 찾을 수 있다는 것을 알았습니다.
결국 우리는 모델의 매개변수를 조정함으로써 손실 함수를 최소화할 수 있습니다.

예를 들어, 이미지에서의 최소값을 찾아보겠습니다.
우리는 SGD 옵티마이저를 10번 동안 실행했습니다.
10 단계 후에 옵티마가 손실 함수 최소값을 거의 찾아냈다는 것을 관찰할 수 있습니다.
우리는 옵티마가 마지막 값에 가까워질수록 가중치가 천천히 작아지는 것을 알 수 있습니다.
2) 학습률의 중요성
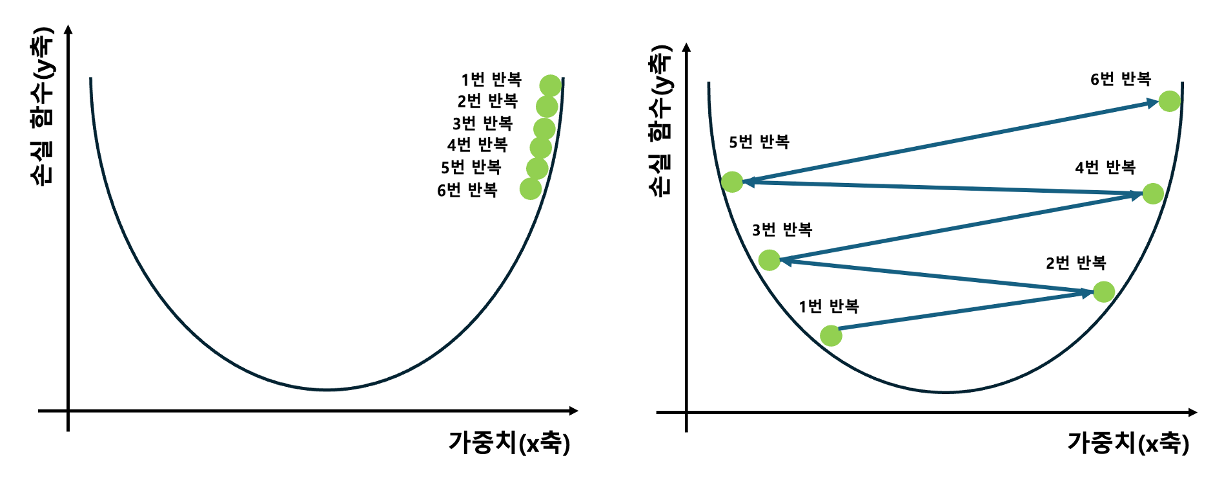
※ 학습률이 너무 낮은 경우
왼쪽 그림을 보면, 학습률이 낮을 때 매개변수의 업데이트가 매우 작게 일어납니다.
각 반복에서 조금씩 이동하면서 손실 함수의 최소값에 접근합니다.
이렇게 작은 단계로 이동하는 것은 가중치 업데이트를 매우 세밀하게 하지만, 문제는 시간이 많이 걸린다는 것입니다.
만약 데이터 세트가 크고 복잡하다면, 학습 과정이 매우 느려서 실용적이지 않을 수 있습니다.
또한, 지역 최소값(Local Minimum)에 빠지기 쉽고, 이를 탈출하기 어려울 수 있습니다.
이러한 이유로, 너무 낮은 학습률은 효율적이지 않을 수 있습니다.
※ 학습률이 너무 높은 경우
오른쪽 그림을 살펴보면, 학습률이 너무 높으면 매개변수가 큰 폭으로 업데이트됩니다.
이는 손실 함수의 최소값을 향해 빠르게 접근할 수 있지만, 동시에 매개변수가 최소값을 지나쳐서 반대편으로 가버릴 수도 있습니다.
이 경우, 알고리즘은 최소값 주변을 왔다 갔다 하면서 발산할 수도 있으며, 최적의 해를 찾지 못하고 끝나버릴 수도 있습니다.
이처럼 너무 높은 학습률은 알고리즘을 불안정하게 만들 수 있습니다.
3) 적절한 학습률 찾기
적절한 학습률을 설정하는 것은 중요합니다.
학습률이 너무 낮지도, 높지도 않게 조절하여 손실 함수의 최소값에 효과적으로 도달할 수 있어야 합니다.
일반적으로는 경험적인 방법, 즉 여러 학습률을 시도해보고 검증 세트에서의 성능을 통해 가장 적합한 학습률을 찾는 것이 유용합니다.
또한, 학습률 스케줄링을 사용하여 학습 과정 중에 학습률을 점진적으로 감소시키는 기법도 있습니다.
4) 학습률의 장단점
장점:
- 학습률 조정을 통해 모델 학습의 효율성을 높일 수 있습니다.
- 적절한 학습률은 학습 과정을 가속화하고, 손실 함수의 최소값을 찾는 데 도움을 줍니다.
단점:
- 학습률이 너무 높으면 최소값을 지나쳐 발산할 수 있습니다.
- 너무 낮은 학습률은 학습 과정을 너무 느리게 하며, 지역 최소값에 갇힐 위험을 증가시킵니다.
5) 코드
선형 모델을 학습률 0.1/0.001로 100번의 에폭(epoch) 동안 훈련하는 과정을 보여줍니다.
각 에폭마다 모델의 예측값을 계산하고, 평균 제곱 오차(Mean Squared Error, MSE) 손실을 사용하여 실제값과의 차이를 계산합니다.
그 다음, 손실에 대한 그래디언트를 계산하고(모델.backward()), 옵티마이저를 사용하여 모델의 파라미터를 업데이트합니다.
두 가지 서로 다른 학습률 설정(0.01과 0.001)을 사용하여 동일한 신경망 모델을 훈련시키고, 각 설정에서의 학습 과정과 결과를 비교하기 위해 작성되었습니다.
여기서 사용된 모델은 nn.Linear(1, 1)로, 입력 특성이 하나이고 출력 또한 하나인 가장 간단한 형태의 선형 회귀 모델입니다.
목표는 모델이 입력 로브로부터 y를 예측하도록 학습시키는 것입니다.
※ 학습률의 역할
학습률은 옵티마이저가 손실 함수의 그래디언트에 기반하여 모델의 가중치를 얼마나 크게 조정할지 결정하는 매개변수입니다. 즉, 학습률이 높으면 가중치 조정이 크게 일어나고, 학습률이 낮으면 가중치 조정이 더 섬세하게 이루어집니다.
※ 학습률 0.01 사용 시
첫 번째 실험에서는 학습률을 0.01로 설정합니다.
이 설정은 비교적 보편적인 초기 선택지 중 하나로, 많은 경우에서 합리적인 수렴 속도와 성능을 제공할 수 있습니다.
학습 과정에서 20 에포크마다 손실을 출력하여 학습이 어떻게 진행되고 있는지 관찰할 수 있습니다.
※ 학습률 0.001 사용 시
두 번째 실험에서는 학습률을 0.001로 줄입니다.
이는 더 조심스럽고 세밀한 가중치 조정을 가능하게 하여, 때로는 더 나은 일반화 성능을 제공할 수 있으나, 학습 속도는 다소 느려질 수 있습니다.
이 경우 역시 20 에포크마다 손실을 출력하여 학습 과정을 관찰합니다.
※ 관찰 가능한 내용
이 두 실험을 통해 학습률이 학습 과정과 모델 성능에 미치는 영향을 관찰할 수 있습니다.
일반적으로 높은 학습률은 빠른 수렴을 가져오지만, 손실 함수에서 최소값을 "넘어서서" 발산할 수 있어 결과적으로 학습이 불안정해질 수 있습니다.
반대로 낮은 학습률은 안정성을 제공하지만, 학습 속도가 느려져 더 많은 에폭 시간이 걸릴 수 있으며, 때로는 지역 최소값에 갇힐 수 있음을 보여줍니다.
import torch
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F
# 학습 데이터 정의
x = torch.tensor([[1.0], [2.0], [3.0]])
y = torch.tensor([[2.0], [4.0], [6.0]])
# 학습률 0.01
print("[1] 학습률이 0.01인 훈련")
model_01 = nn.Linear(1, 1)
optimizer_01 = optim.SGD(model_01.parameters(), lr=0.01)
for epoch in range(100):
pred = model_01(x)
loss = F.mse_loss(pred, y)
optimizer_01.zero_grad()
loss.backward()
optimizer_01.step()
if (epoch+1) % 20 == 0:
print(f'Epoch {epoch+1}, Loss: {loss.item()}')
print("\n") # 결과를 구분하기 위해 빈 줄 출력
# 학습률 0.001
print("[2] 학습률이 0.001인 훈련")
model_001 = nn.Linear(1, 1)
optimizer_001 = optim.SGD(model_001.parameters(), lr=0.001)
for epoch in range(100):
pred = model_001(x)
loss = F.mse_loss(pred, y)
optimizer_001.zero_grad()
loss.backward()
optimizer_001.step()
if (epoch+1) % 20 == 0:
print(f'Epoch {epoch+1}, Loss: {loss.item()}')[1] 학습률이 0.01인 훈련
Epoch 20, Loss: 0.40318718552589417
Epoch 40, Loss: 0.011412662453949451
Epoch 60, Loss: 0.007148616015911102
Epoch 80, Loss: 0.006463317200541496
Epoch 100, Loss: 0.005869826767593622
[2] 학습률이 0.001인 훈련
Epoch 20, Loss: 8.46878433227539
Epoch 40, Loss: 5.493402004241943
Epoch 60, Loss: 3.588287591934204
Epoch 80, Loss: 2.3682148456573486
Epoch 100, Loss: 1.5866127014160156
※ 결과 해석
※ 학습률이 0.01인 훈련
- 빠른 손실 감소: 학습률이 0.01인 경우, 이미 초기 20 에포크에서 손실이 크게 감소하며(약 0.616에서 0.082로), 이후 에포크에서도 꾸준히 감소하는 것을 볼 수 있습니다. 이는 상대적으로 높은 학습률로 인해 모델이 빠르게 최적의 가중치 값으로 수렴하고 있음을 나타냅니다.
- 안정적인 수렴: 100 에포크까지 손실이 점진적으로 줄어들며 모델이 안정적으로 최적화되고 있음을 보여줍니다. 최종 손실이 약 0.058 수준으로 줄어든 것은 모델이 데이터를 잘 학습하고 있음을 의미합니다.
※ 학습률이 0.001인 훈련
- 느린 손실 감소: 학습률이 0.001인 경우, 손실 감소 속도가 현재보다 느린 것을 볼 수 있습니다. 초기 20 에포크에서 손실이 여전히 높은 상태(약 13.03)에서 시작하며, 100 에포크까지도 손실이 2.43 수준으로 남아 있습니다. 이는 낮은 학습률로 인해 가중치 조정이 더디게 이루어지고 있음을 나타냅니다.
- 점진적인 개선: 학습 과정이 느리긴 하지만, 에포크 진행에 따라 손실이 지속적으로 줄어들고 있음을 확인할 수 있습니다. 이는 모델이 점차 최적화되고 있으며, 더 많은 에포크를 통해 손실을 더 줄일 수 있음을 시사합니다.
※ 종합적인 해석
- 학습률과 학습 속도의 관계: 이 결과는 학습률이 모델의 학습 속도와 수렴 속도에 큰 영향을 미친다는 것을 보여줍니다. 높은 학습률(0.01)은 빠른 학습 속도를 가능하게 하지만, 너무 높으면 학습이 불안정해질 수 있습니다. 반면, 낮은 학습률(0.001)은 학습을 더 안정적으로 만들 수 있지만, 수렴 속도가 느려 더 많은 에포크 시간이 필요할 수 있습니다.
- 적절한 학습률의 중요성: 적절한 학습률을 설정하는 것은 모델의 효율적인 학습과 수렴에 매우 중요합니다. 너무 높거나 낮은 학습률은 학습 과정에 부정적인 영향을 미칠 수 있으므로, 여러 실험을 통해 최적의 값을 설정하고 가장 적합한 학습 과정을 유지해야 합니다.
'딥러닝 > 딥러닝: 기초 개념' 카테고리의 다른 글
| 파이썬을 활용한 순방향 전파로 집 가격 예측 (1) | 2025.01.15 |
|---|---|
| 옵티마이저와 드롭아웃 (0) | 2025.01.15 |
| 손실 함수의 미분 (0) | 2025.01.14 |
| 오차 역전파법과 손실함수 (0) | 2025.01.14 |
| 활성화 함수 (1) | 2025.01.13 |