1. 딥러닝으로 풀어내는 집 가격 예측의 기초
집을 구매하거나 판매할 때, '이 집은 얼마일까?'하는 가격 예측은 중요한 부분입니다.
집 가격을 예측하기 위해 고려해야 할 요소로는 그 지역의 생활 수준, 주변의 공원이나 상점 같은 환경, 집의 크기, 몇 년 됐는지, 집 안의 꾸밈 상태 같은 여러 가지를 봐야 합니다.
기존의 방법들, 예를 들면 선형 회귀와 같은 통계적 모델들은 이러한 복잡한 요소들을 독립적으로만 고려하기 때문에 정확한 예측을 하는 데 한계가 있습니다.
여기서 딥러닝이 큰 역할을 합니다.
딥러닝은 신경망이라는 특별한 구조를 사용하는데, 신경망은 사람의 뇌가 정보를 처리하는 방식을 모방한 것입니다.
데이터간의 상호작용을 효과적으로 처리하고, 여러 층을 통해 복잡한 데이터 구조를 학습하는 능력을 갖추고 있어, 다양한 데이터를 함께 고려하면서 복잡한 문제를 해결할 수 있습니다.
신경망은 크게 세 가지 부분으로 구성됩니다
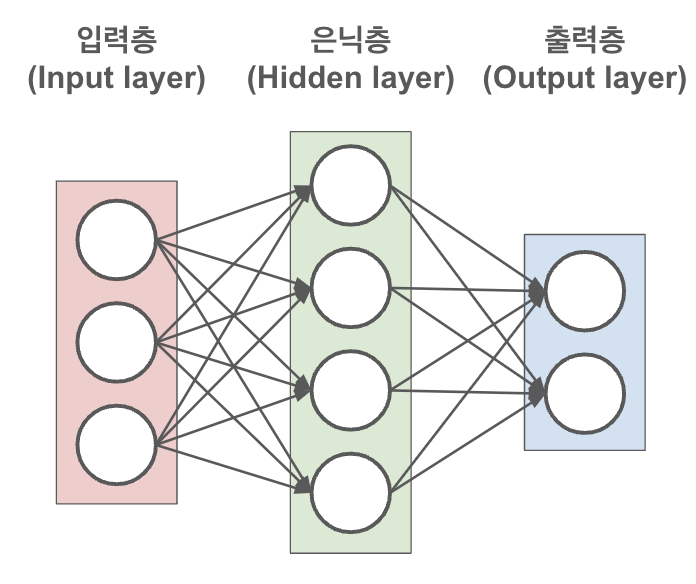
- 입력층(Input Layer): 여기서는 집 가격을 맞추기 위해 필요한 모든 정보를 모읍니다. 이 정보에는 그 집이 어디에 있는지, 얼마나 큰지, 몇 살인지, 안의 상태는 어떤지 등이 포함됩니다.
- 은닉층(Hidden Layers): 이 층에서는 '데이터 처리 과정'이 일어납니다. 입력된 정보가 결합되고 변형되면서 집 가격에 영향을 미치는 패턴이나 주요 요소들에 대한 새로운 통찰을 찾아냅니다.
- 출력층(Output Layer): 마지막 단계에서는 모든 분석 결과를 종합해서 '이 집의 가격은 대략 이 정도일 거야'라는 최종 예측합니다.
2. 신경망을 통한 순방향 전파로 집 가격 예측 이해
순방향 전파란, 신경망이 우리가 준 정보를 받아서 그 결과를 계산하는 과정을 말합니다.
정보들은 입력층에서 시작해 은닉층을 거쳐 마지막으로 출력층에서 결과를 내놓습니다.
부동산 시장에서는 어떤 집의 가격을 예측하기 위해, 집의 크기, 방의 개수를 살펴봅니다.
예를 들어 도심에 있는 30평 크기의 집이 2개의 방을 갖고 있다고 해보면 우리는 이 정보를 신경망을 통해 처리하고 집의 가격을 예측해 볼 수 있습니다.
이제 이 정보들은 신경망의 첫 번째 단계인 입력층으로 들어갑니다.
그리고 나서, 이 정보들은 은닉층을 거치면서 처리되는데, 여기서 가중치라는 개념이 중요한 역할을 합니다.
예를 들어, 만약 방의 개수가 집 가격에 더 많은 영향을 미친다고 여겨진다면, 방의 개수에 연결된 가중치는 집의 크기에 연결된 가중치보다 크게 설정됩니다.
즉, 가중치의 크기는 해당 정보가 예측 결과에 얼마나 큰 영향을 주는지를 나타내는 지표가 됩니다.
첫 번째 은닉 노드의 값을 계산하려면, 입력 값들(집의 크기, 방의 개수)에 해당하는 가중치를 곱한 다음 그 결과를 모두 더합니다.
즉, (30 x 가중치1) + (2 x 가중치3) 와 같은 계산을 하게 됩니다.
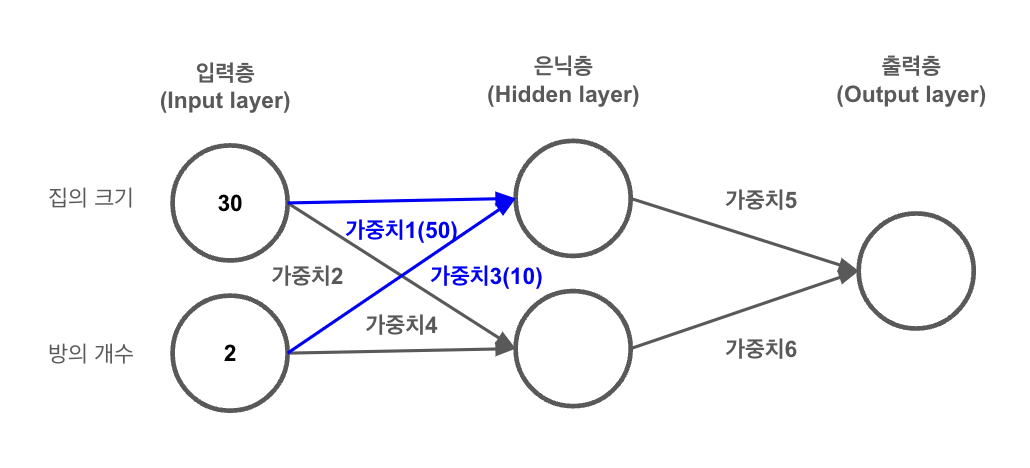
이제, 이 과정을 은닉층의 모든 노드에 적용한 뒤, 이를 통해 얻은 결과를 사용해 출력층에서 최종적인 집의 가격을 예측합니다.
출력층에서도 은닉층의 결과에 가중치를 곱하여 최종 예측값을 도출합니다.
3. 순방향 전파를 활용한 집 가격 예측 실습
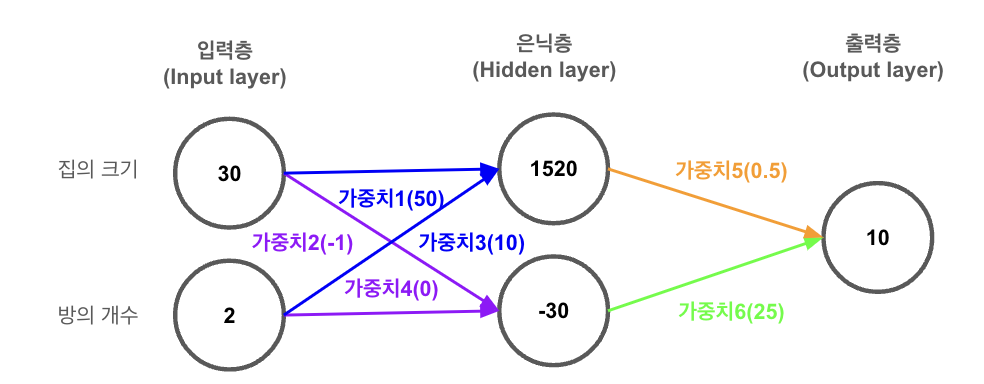
- 집의 크기가 30평, 방의 개수가 2개
- 은닉층 첫 번째 노드의 가중치: 50, 10
- 은닉층 두 번째 노드의 가중치: -1, 0
- 출력층 가중치: 0.5, 25
예측을 위해 다음과 같은 계산을 수행합니다.
1) 은닉층(Hidden layer)
- 첫 번째 노드: (30 x 50) + (2 x 10) = 1500 + 20 = 1520
- 두 번째 노드: (30 x -1) + (2 x 0) = -30 + 0 = -30
따라서 은닉층에서 노드의 값은 1520과 -30이 됩니다.
2) 출력층(Output Layer)
- (1520 x 0.5) + (-30 x 25) = 760 - 750 = 10
집의 크기가 30평, 방의 개수가 2개인 집의 가격은 10억이라고 예측했습니다.
이 모든 과정이 바로 '순방향 전파'라는 것 입니다.
쉽게 말해, 신경망은 우리가 주는 데이터를 받아서 가중치를 이용해 계산하고, 그 결과를 바탕으로 예측을 해냅니다.
이 과정은 데이터 포인트에 대해 하나씩 진행되고, 마지막 층에서 나온 값이 바로 그 데이터에 대한 신경망의 예측입니다.
4. 순방향 전파를 활용한 집 가격 예측 코드 실습
input_data = [30, 2] # 집의 크기가 30평, 방의 개수가 2개
weights = {
'node_0': [50, 10], # 은닉층 첫 번째 노드의 가중치
'node_1': [-1, 0], # 은닉층 두 번째 노드의 가중치
'output': [0.5, 25] # 출력층 가중치
}
# 은닉층 첫 번째 노드 계산
node_0_value = input_data[0] * weights['node_0'][0] + input_data[1] * weights['node_0'][1]
# 은닉층 두 번째 노드 계산
node_1_value = input_data[0] * weights['node_1'][0] + input_data[1] * weights['node_1'][1]
# 은닉층 결과
hidden_layer_values = [node_0_value, node_1_value]
print(f"은닉층 결과 출력:",hidden_layer_values)
# 출력층에서의 최종 예측
output = hidden_layer_values[0] * weights['output'][0] + hidden_layer_values[1] * weights['output'][1]
# 결과 출력
print(f"예측된 집의 가격: {int(output)}억")은닉층 결과 출력: [1520, -30]
예측된 집의 가격: 10억5.순방향 전파를 활용한 예측 문제

# 입력 데이터와 가중치 설정
input_data = [10, 2]
weights = {
'node_0': [0.5, 1],
'node_1': [-1, 0],
'output': [1, 0.5]
}
# 은닉층 노드 계산
node_0_value = input_data[0] * weights['node_0'][0] + input_data[1] * weights['node_0'][1]
node_1_value = input_data[0] * weights['node_1'][0] + input_data[1] * weights['node_1'][1]
hidden_layer_values = [node_0_value, node_1_value]
# 출력층 최종 예측
output = hidden_layer_values[0] * weights['output'][0] + hidden_layer_values[1] * weights['output'][1]
print(f"예측값: {output}")예측값: 2.06. 활성화 함수(Activation Functions): 신경망의 비선형 특성
신경망의 은닉층에서 일어나는 연산이 단순한 곱셈과 덧셈에 불과하다고 생각할 수 있지만, 신경망의 진정한 지능은 활성화 함수를 통해 비로소 발휘됩니다.
활성화 함수는 신경망에 비선형적인 특성을 부여해, 세상을 보다 복잡하고 다차원적으로 인식할 수 있게 해줍니다.
예를 들어, 집의 가격을 예측하는 모델을 생각해보겠습니다.
단순히 방의 개수가 많고, 평수가 크다고 해서 가격이 선형적으로 증가하지 않습니다.
방이 1개인 집과 3개인 집의 가격 차이는 그 개수 차이만으로 설명할 수 없고, 10평과 50평인 집의 가격 또한 다양한 요인에 의해 결정됩니다.
활성화 함수는 이러한 비선형적인 관계를 모델링하여 신경망이 이런 복잡한 패턴을 파악하고 학습할 수 있도록 돕습니다.
가장 인기 있는 활성화 함수 중 하나인 ReLU(Rectified Linear Unit)는 입력값이 음수일 때는 0을 반환하고, 양수일 때는 입력값을 그대로 반환하는 비선형 함수입니다.
이는 깊은 신경망에서 특히 그 성능을 발휘합니다.

7. 은닉층의 중요성: 신경망의 다층 구조와 복잡한 패턴 학습
신경망에 은닉층을 추가하는 것은 건물에 층을 추가하는 것과 유사합니다.
한 층만 있는 건물보다 여러 층이 있는 건물이 더 많은 것을 수용할 수 있듯이, 여러 은닉층을 쓰면 신경망이 더 많은 정보를 배우고 처리할 수 있습니다.
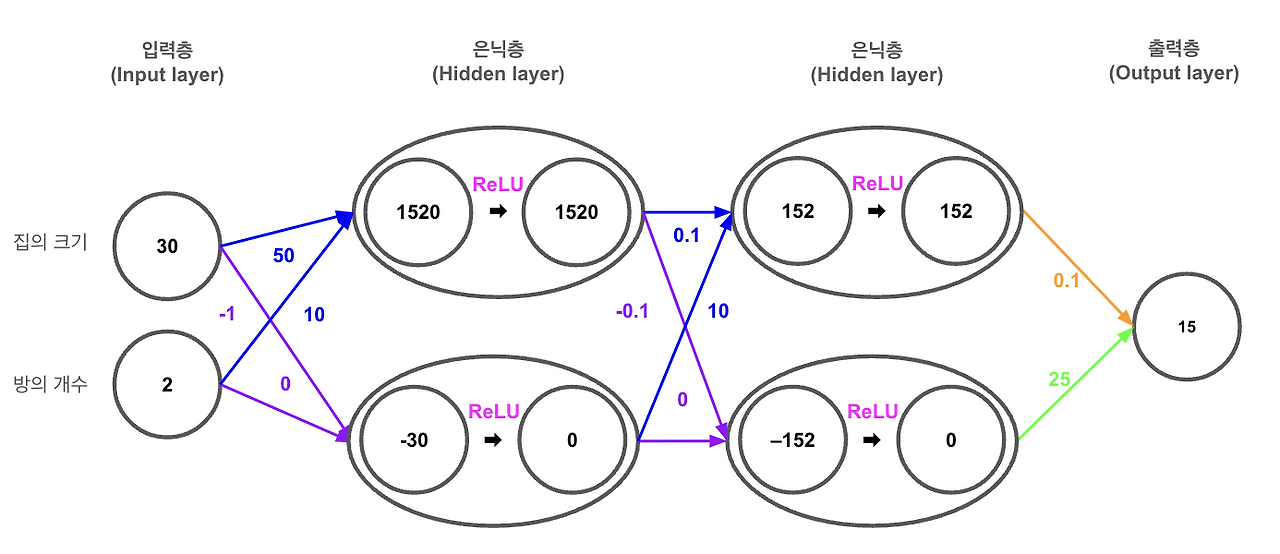
이제, 두 개의 은닉층을 가진 신경망을 통해 ReLU 활성화 함수가 실제로 어떻게 작동하는지 살펴보겠습니다.
- 집의 크기가 30평, 방의 개수가 2개
- 첫 번째 은닉층 첫 번째 노드의 가중치: 50, 10
- 첫 번째 은닉층 두 번째 노드의 가중치: -1, 0
- 두 번째 은닉층 첫 번째 노드의 가중치: 0.1, 10
- 두 번째 은닉층 두 번째 노드의 가중치: -0.1, 0
- 출력층 가중치: 0.1, 25
예측을 위해 다음과 같은 계산을 수행합니다.
1) 입력층(Input Layer):
- 입력값은 집의 크기가 30평, 방의 개수가 2개입니다.
2) 첫 번째 은닉층(First Hidden Layer):
- 첫 번째 노드: (30 x 50) + (2 x 10) = 1500 + 20 = 1520 입니다. 1520은 양수이므로 ReLU 함수를 적용하면 1520이 됩니다.
- 두 번째 노드: (30 x -1) + (2 x 0) = -30 + 0 = -30 입니다. -30은 음수이므로 ReLU 함수를 적용하면 0이 됩니다.
따라서 첫 번째 은닉층에서 노드의 값은 1520과 0이 됩니다.
3) 두 번째 은닉층(Second Hidden Layer):
- 첫 번째 노드: (1520 x 0.1) + (0 x 10) = 152 입니다. ReLU 함수를 적용하면 152 가 됩니다.
- 두 번째 노드: (1520 x -0.1) + (0 x 0) = -152 입니다. ReLU를 함수를 적용하면 0이 됩니다.
따라서 두 번째 은닉층에서 노드의 값은 152와 0이 됩니다.
4) 출력층(Output Layer):
- (152 x 0.1) + (0 x 25) = 15.2 입니다. 이 값은 소수점을 고려하여 약 15 가 됩니다.
따라서 집의 크기가 30평이고, 방의 개수가 2개인 데이터를 신경망 모델로 예측한 가격값은 15억 입니다.
이 예시를 통해 보듯이, 각 은닉층과 활성화 함수는 입력 데이터의 복잡한 특성을 신경망이 이해하고 학습할 수 있도록 변환하는 데 핵심적인 역할을 합니다.
최종적으로, 이 모델은 주어진 입력에 대해 약 15의 값을 출력하며, 이는 신경망이 데이터로부터 학습한 패턴을 기반으로 한 추론 결과입니다.
8. 다층 신경망과 ReLU 활성화 함수를 사용한 집 가격 예측 실습
def relu(x):
"""ReLU 활성화 함수"""
return max(0, x)
# 입력 데이터 설정
input_data = [30.0, 2.0]
# 가중치 설정
weights = {
'hidden1_node0': [50.0, 10.0],
'hidden1_node1': [-1.0, 0.0],
'hidden2_node0': [0.1, 10.0],
'hidden2_node1': [-0.1, 0.0],
'output': [0.1, 25.0]
}
# 첫 번째 은닉층 계산 및 ReLU 활성화 함수 적용
hidden1_node0_output = input_data[0] * weights['hidden1_node0'][0] + input_data[1] * weights['hidden1_node0'][1]
hidden1_node0_activated = relu(hidden1_node0_output)
hidden1_node1_output = input_data[0] * weights['hidden1_node1'][0] + input_data[1] * weights['hidden1_node1'][1]
hidden1_node1_activated = relu(hidden1_node1_output)
# 두 번째 은닉층 계산 및 ReLU 활성화 함수 적용
hidden2_node0_output = hidden1_node0_activated * weights['hidden2_node0'][0] + hidden1_node1_activated * weights['hidden2_node0'][1]
hidden2_node0_activated = relu(hidden2_node0_output)
hidden2_node1_output = hidden1_node0_activated * weights['hidden2_node1'][0] + hidden1_node1_activated * weights['hidden2_node1'][1]
hidden2_node1_activated = relu(hidden2_node1_output)
# 출력층 계산
output = hidden2_node0_activated * weights['output'][0] + hidden2_node1_activated * weights['output'][1]
# 결과 출력
print(f"예측된 집의 가격: {int(output)}억")예측된 집의 가격: 15억
'딥러닝 > 딥러닝: 기초 개념' 카테고리의 다른 글
| Pytorch의 텐서 연산을 활용하여 단순 선형 회귀 모델 구현 (0) | 2025.01.16 |
|---|---|
| 파이썬을 활용한 모델 학습 최적화와 역방향 전파 (0) | 2025.01.15 |
| 옵티마이저와 드롭아웃 (0) | 2025.01.15 |
| 경사하강법과 학습률 (0) | 2025.01.14 |
| 손실 함수의 미분 (0) | 2025.01.14 |